GAMES102-12-几何映射 & 几何优化

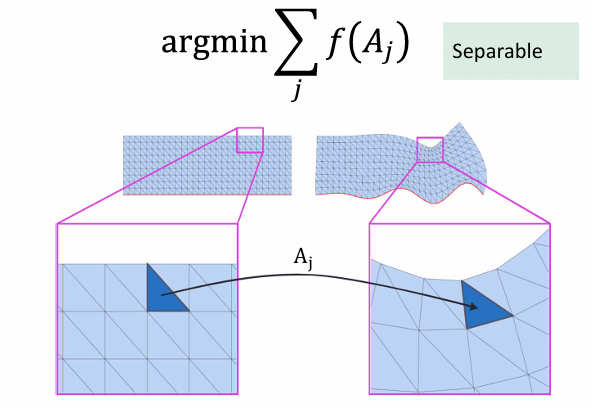
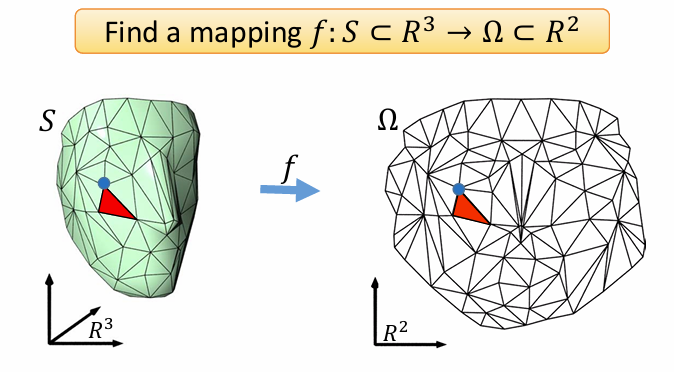
Lecture 12 Geometric Mapping & Geometry Optimization

映射：

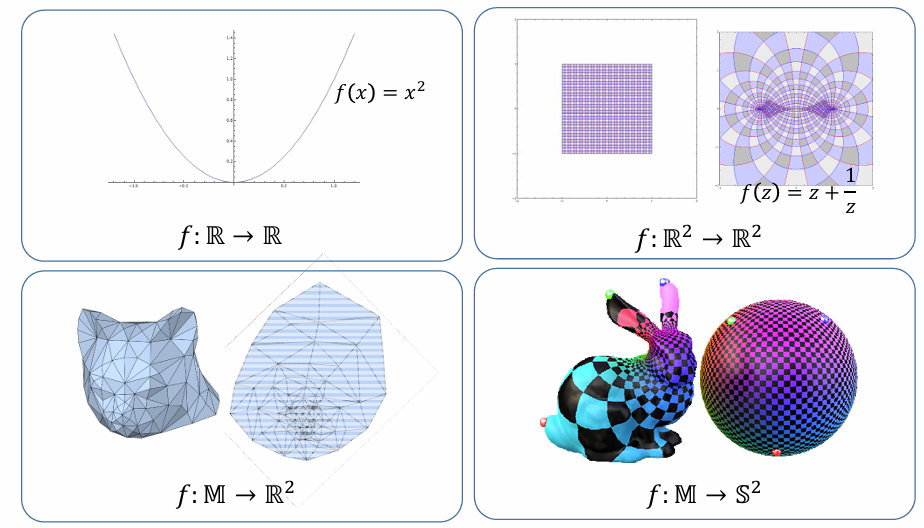
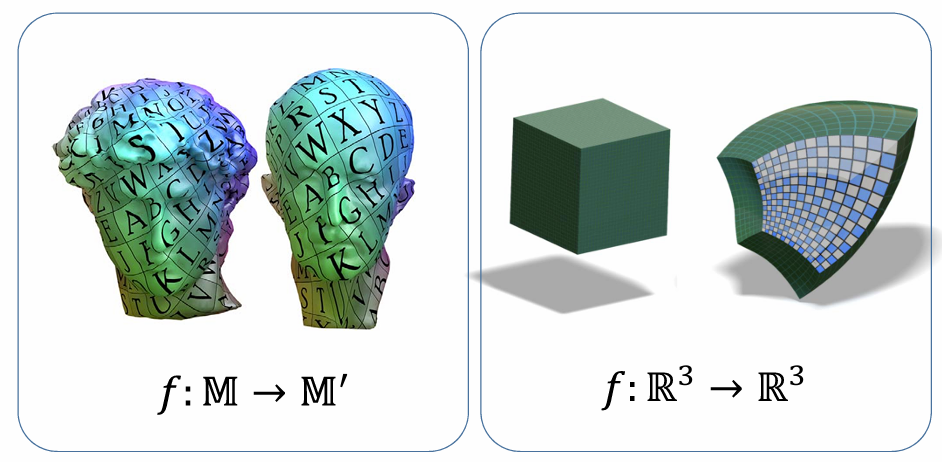
这节课的主要内容是平面几何映射：R² → R²

映射表达：

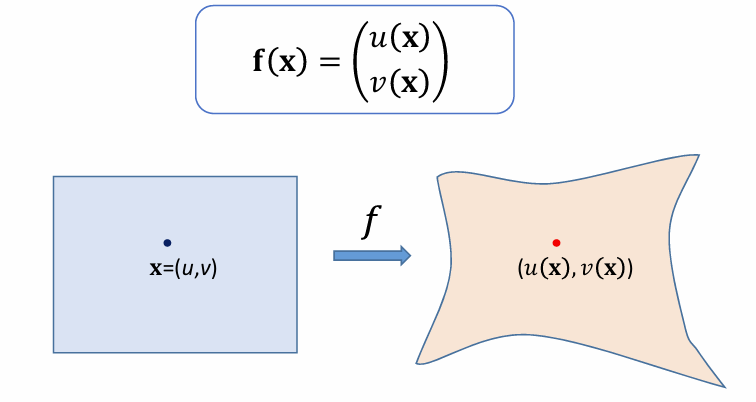
• 映射表达为基本映射（基函数）的线性组合
  • 函数的分解
  • 基函数的线性组合：

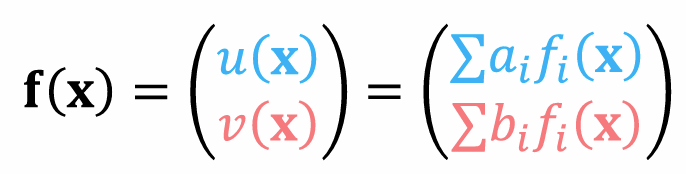
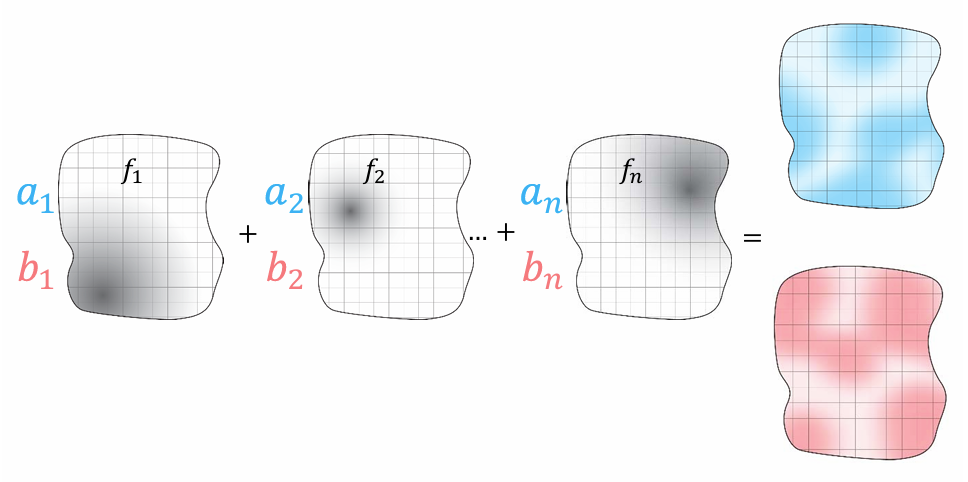
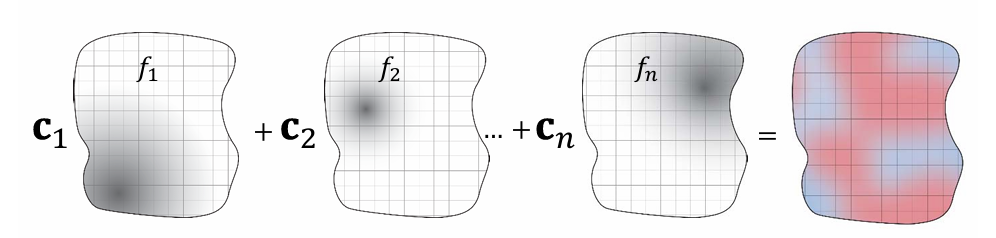
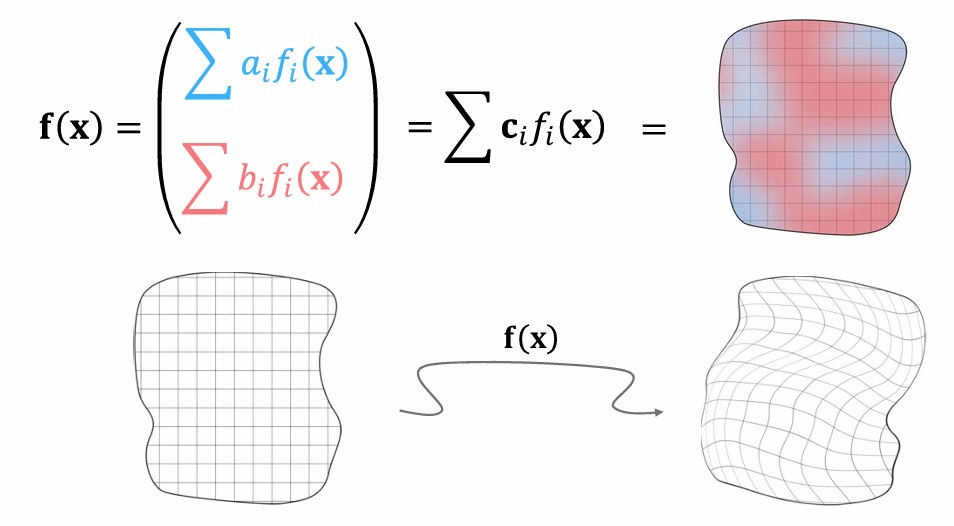
• 映射表达为小区域（三角形区域）上映射的拼接
  • 区域的分解（映射的离散）
  • 简单区域上映射的连续组合

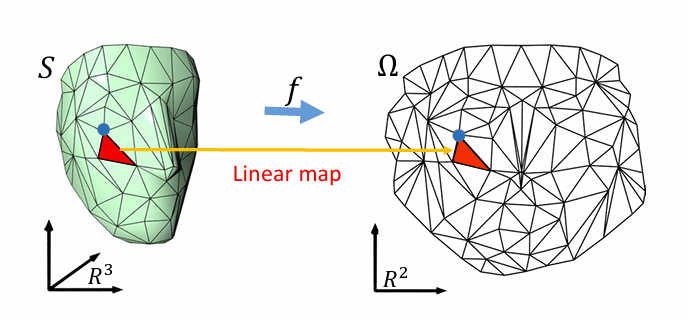
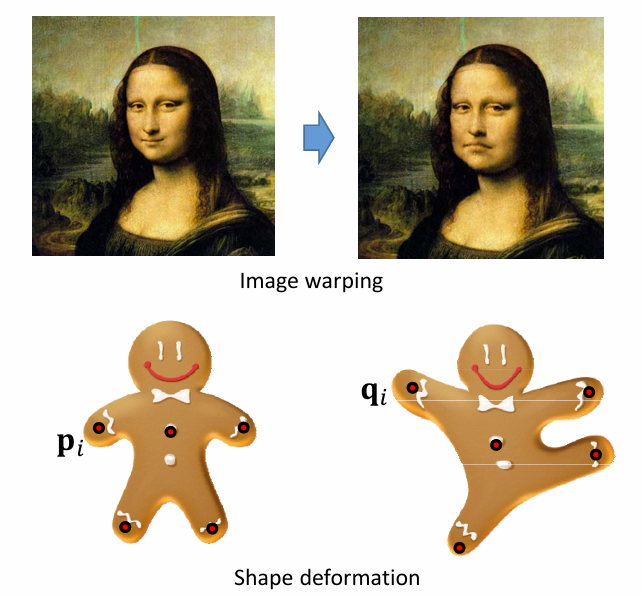
几何映射的例子：

• 2D变形
  • 本质：插值问题
  • 求解方法：
    • 插值法（如RBF插值）
    • 逼近法（能量极小法）

• Barycentric Coordinates（质心坐标）

  

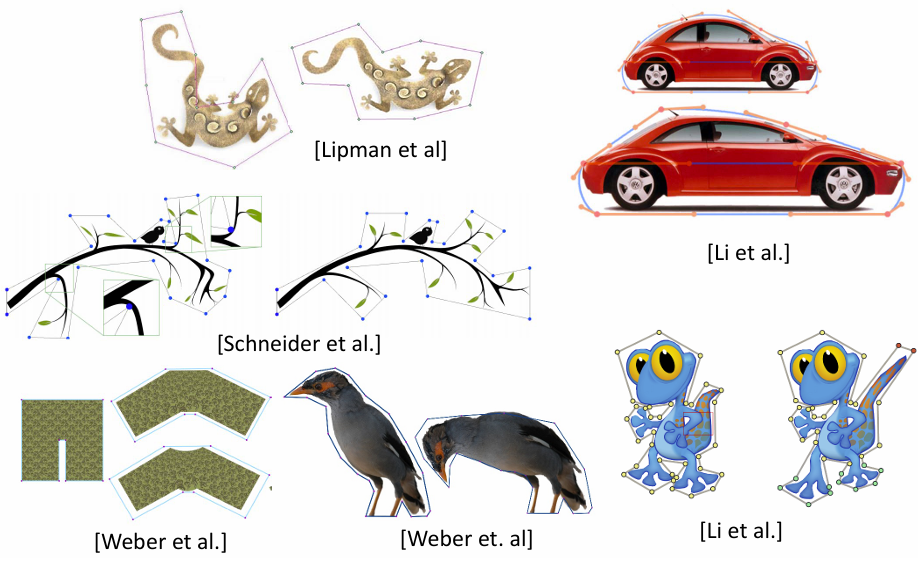
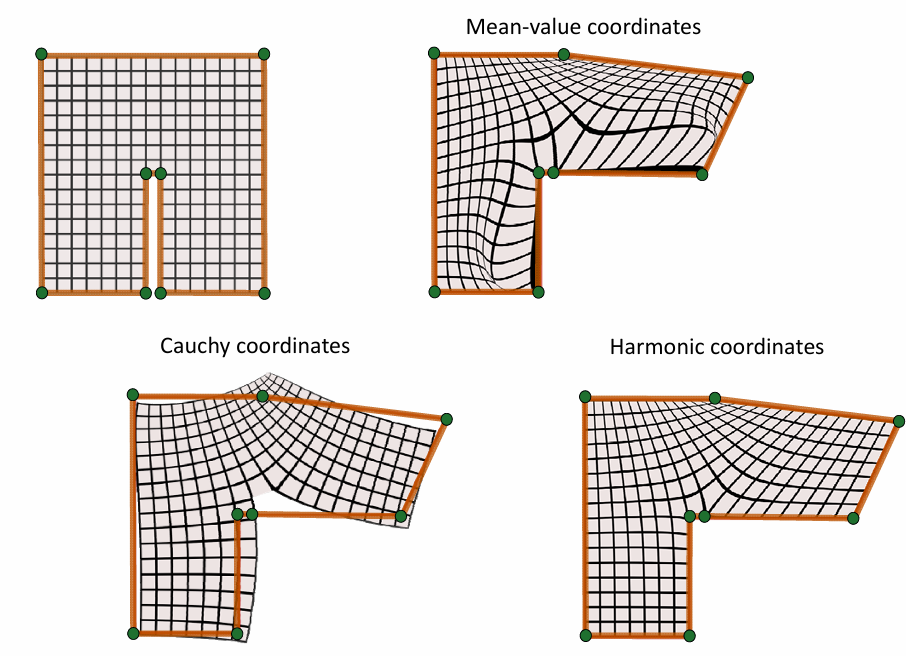
映射的性质

评价方式：双射和扭曲

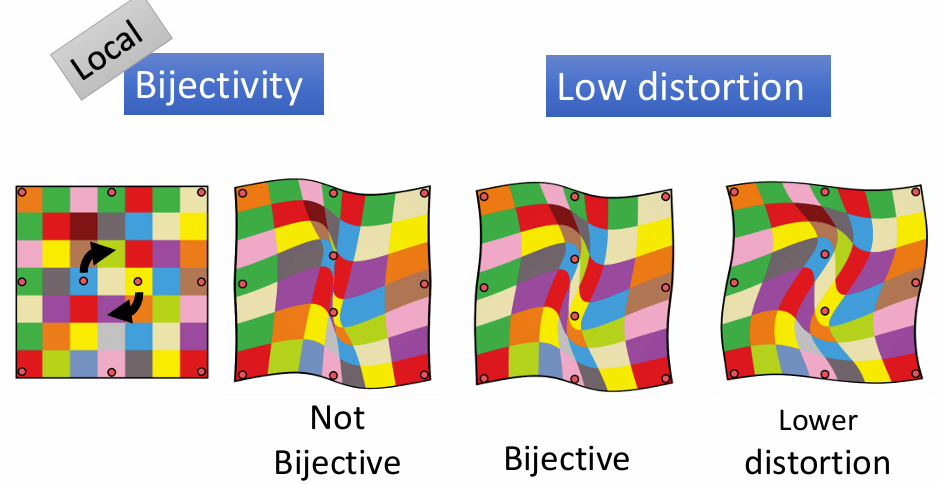
判断是否发生了翻转：看雅可比行列式

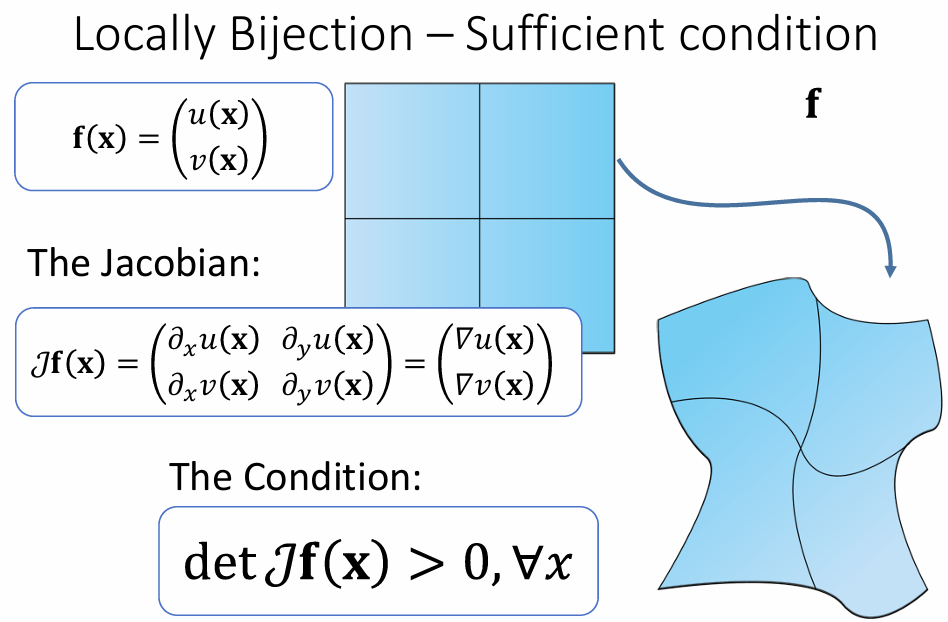
局部双射和全局双射：

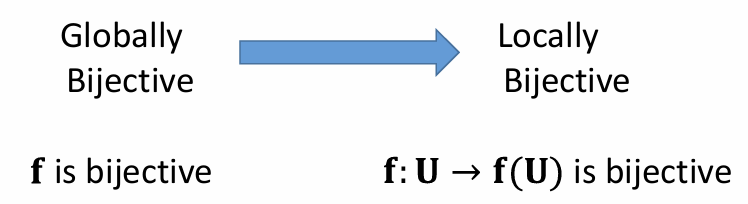
Jacobian的几何意义：

• 函数在某点的Jacobian度量了其局部的形变量

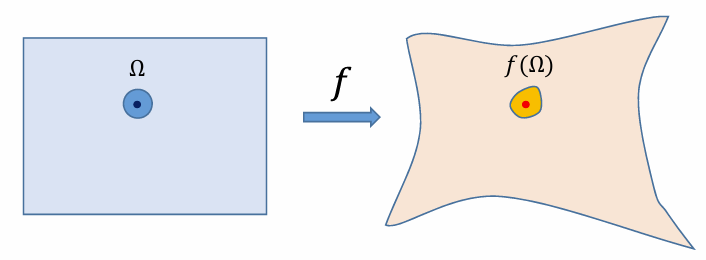
扭曲度量：

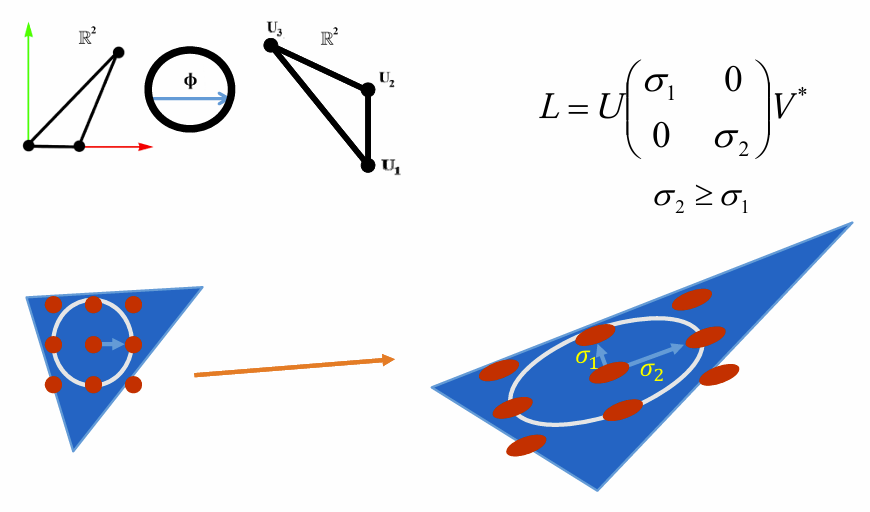
映射的优化模型

约束优化：

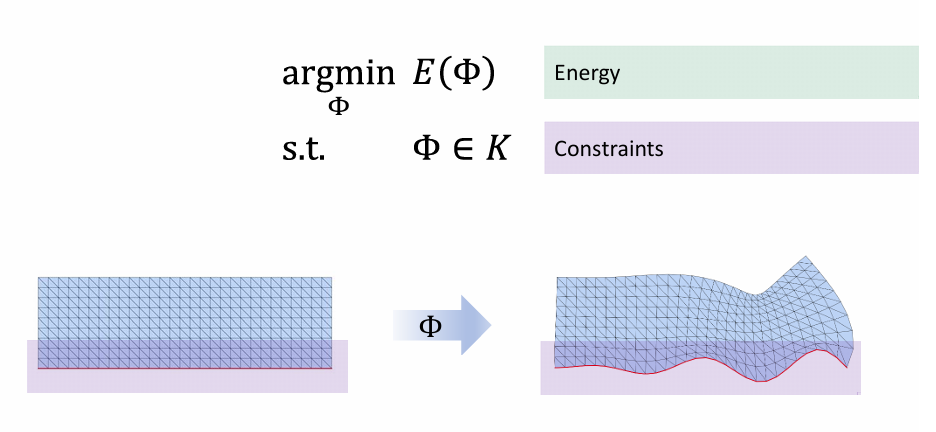
几何优化的求解

能量函数常用：

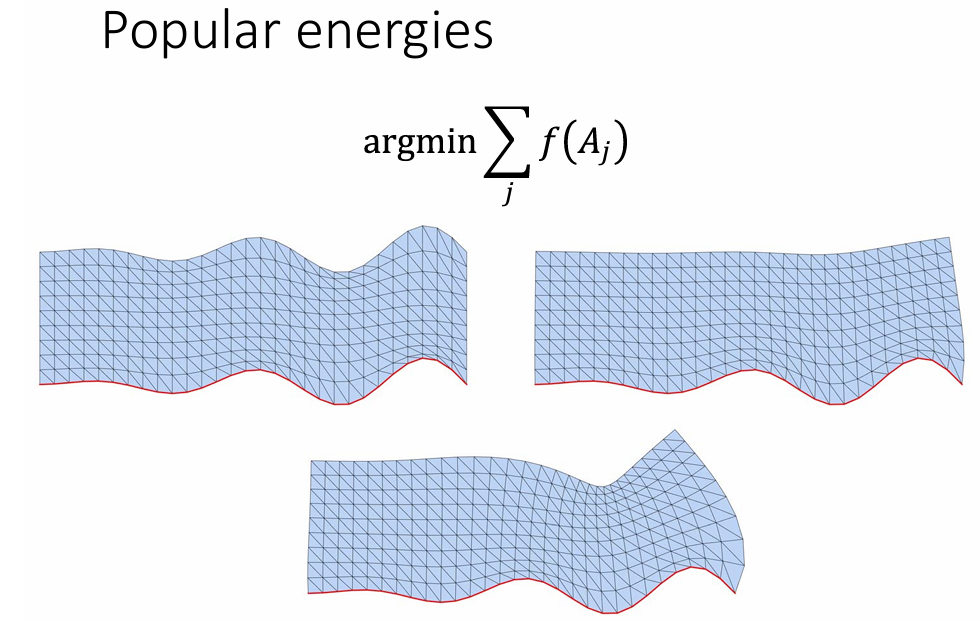
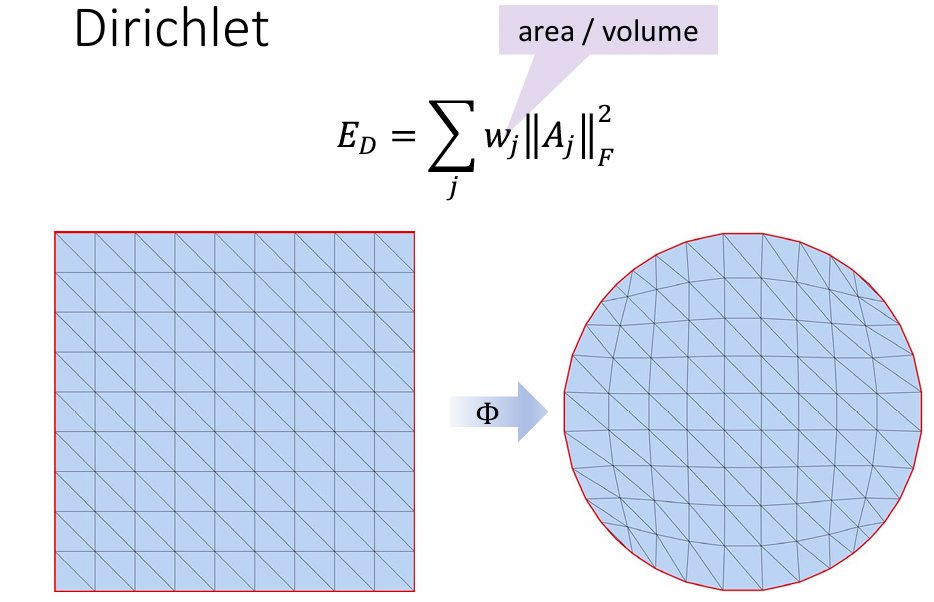
狄利克雷能量：

还有一些其它的方法：

几何优化

对于一般的函数来说，函数导数值为0的点不一定是极值点，也可能是驻点：

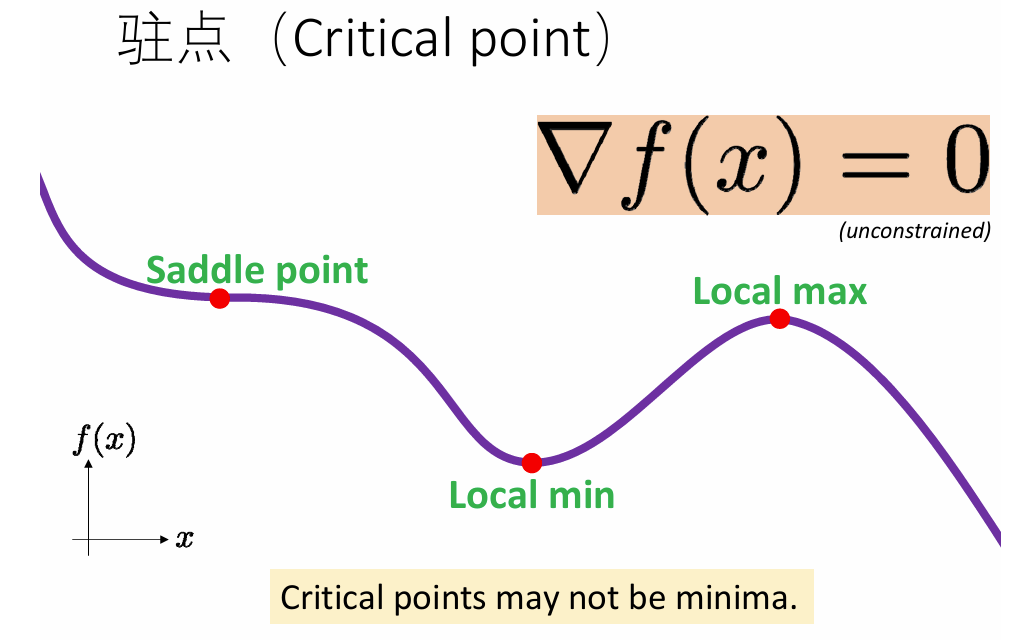
但凸函数的驻点就是最小值。

优化问题类型：

• 有约束/无约束
• 线性/非线性
• 全局/局部
• 凸/非凸
• 连续/离散
• 随机/确定性
• 单目标/多目标

无约束的优化问题

min_xf(x)

• 梯度下降法 (Gradient descent)
• 牛顿法(Newton’s method)
• 拟牛顿法(Quasi‐Newton)
• 坐标下降法(Coordinate descent)

等式约束的优化问题

拉格朗日乘数法

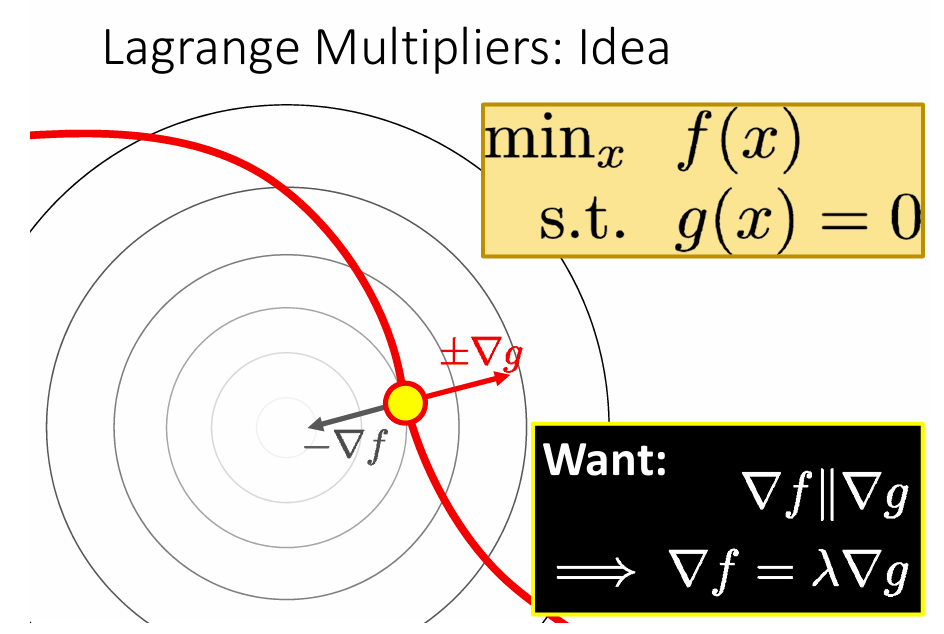
不等式约束的优化问题

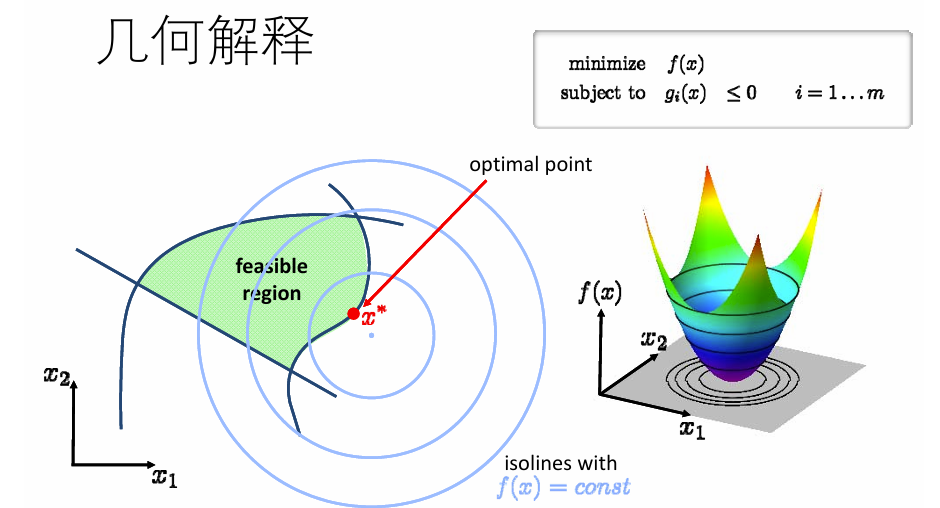
Convex Optimization 凸优化

凸函数能保证找到全局最小值

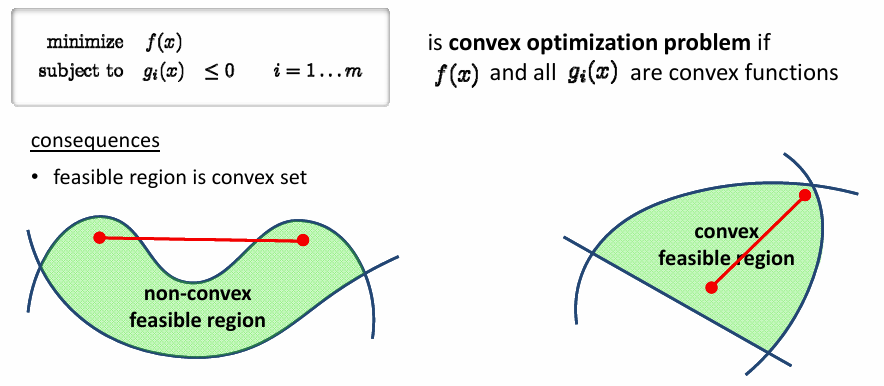
凸优化的主要方法：

• 线性规划
• 二次规划
• 锥规划
• 半定规则

其它优化问题：

• 非线性最小二乘

  

• 混合整数优化

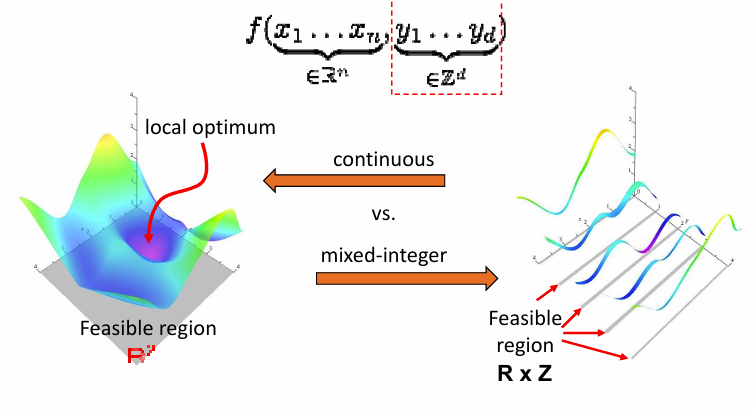
几何处理中的优化问题：具有特殊的几何结构，往往能有特殊的优化方法