Lecture 11 Surface Parameterization & Surfaces Simplification
曲面参数化(又称曲面展开)
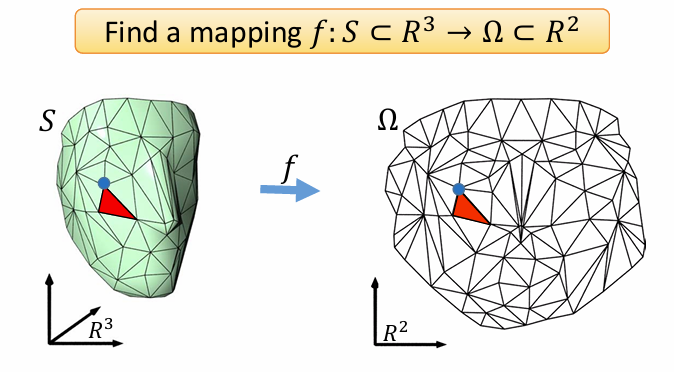
问题:给定一张曲面,如何找其二维的参数定义域?
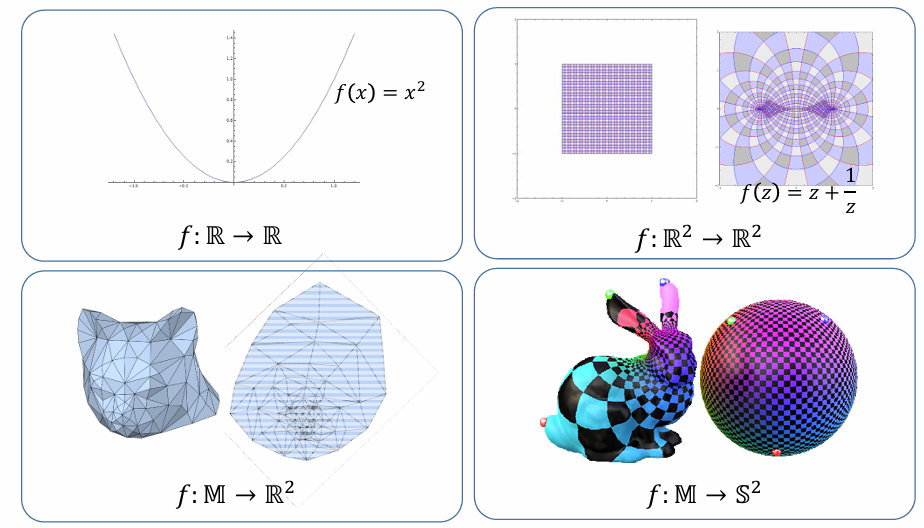
参数化的应用:
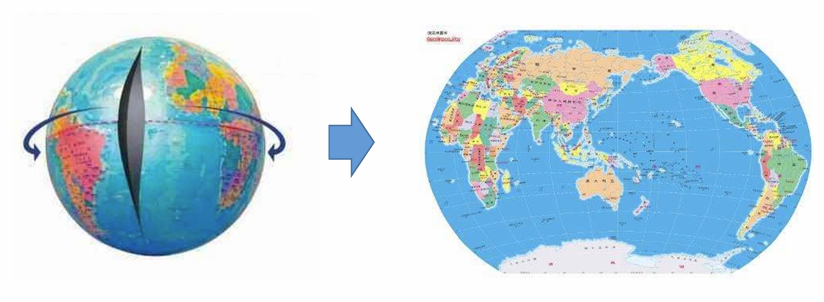
- 地图绘制(地理学)
- 纹理映射
- 曲面绘画
- 大部分几何处理的基础(基本问题)
参数化期望保持的几何性质:
- 保角映射(angle‐preserving):conformal(共形)
- 保面积映射(area‐preserving):authalic
- 等距映射(isometric):conformal + authalic
等轴展开:
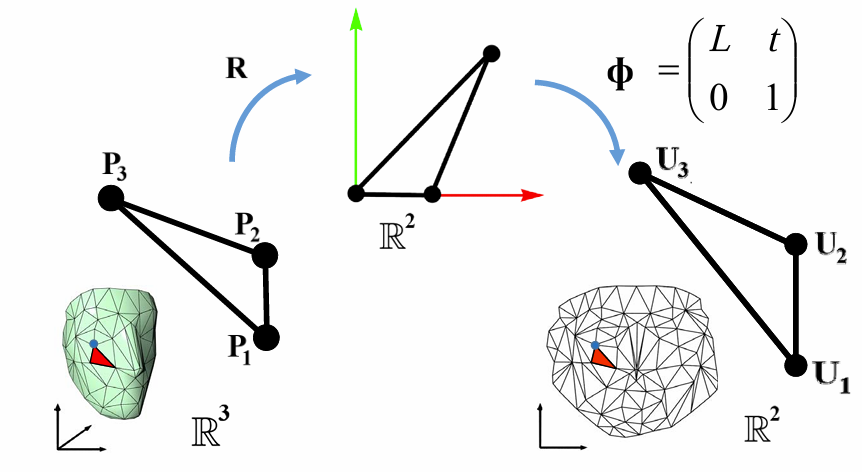
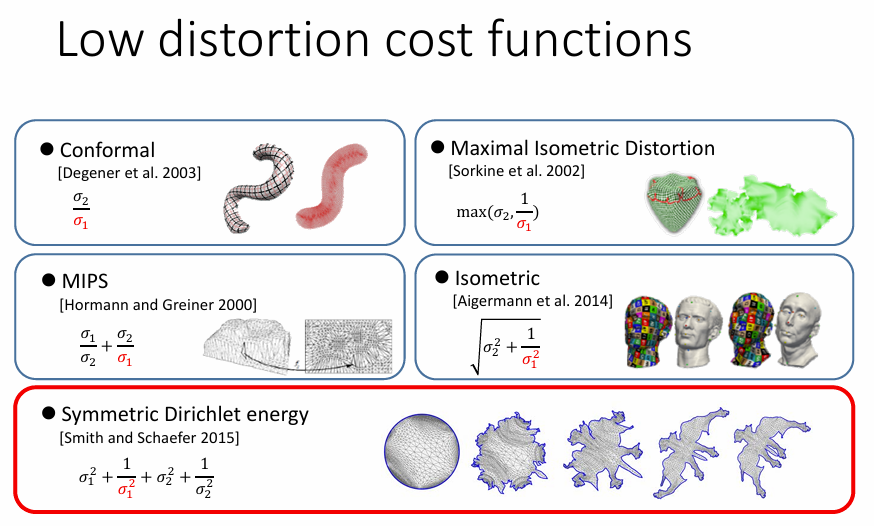
失真度量:
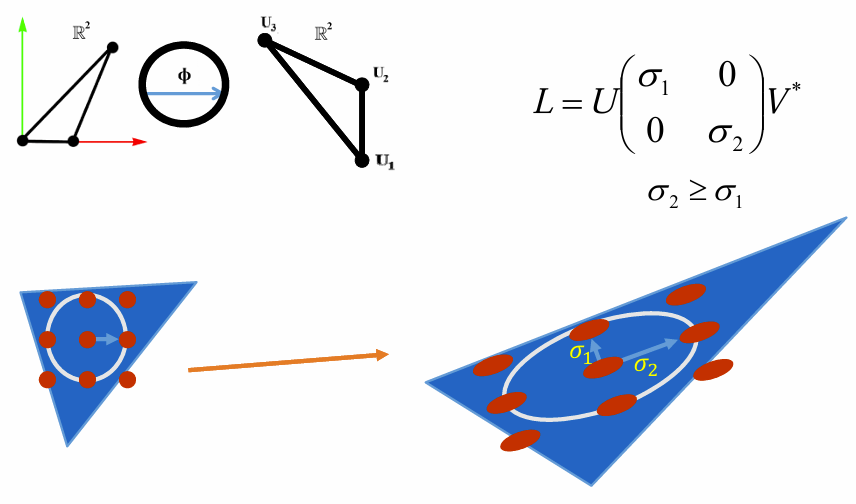
- angle-preserving (conformal) :σ1 = σ2
- area-preserving (authalic) :σ1σ2 = 1
- length-preserving (isometric) :
曲面参数化的方法:
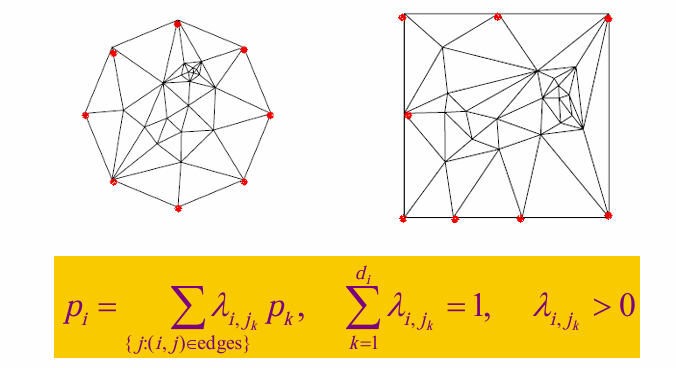
Tutte’s embedding method:将三角剖分映射到凸边界内的方法。(适用于平面图(即可以嵌入到平面上的图)以及更一般的,嵌入到球面或其他曲面上的图)
- 面着色:首先,图的每个面都被分配一个颜色。在平面图中,通常使用两种颜色(双色)来确保相邻的面颜色不同。
- 顶点标记:然后,根据相邻面的颜色,为每个顶点分配一个标记。这个标记可以是0、1或2,取决于相邻面颜色的变化。
- 边的定向:接着,根据顶点的标记,为每条边分配一个方向。这个方向可以是正向或反向,取决于顶点标记的奇偶性。
- 构建嵌入:最后,使用这些信息来构建图的嵌入。这涉及到在表面上放置顶点,并以一种方式绘制边,使得它们不相交,并且每个面的边界都由边正确地定义。
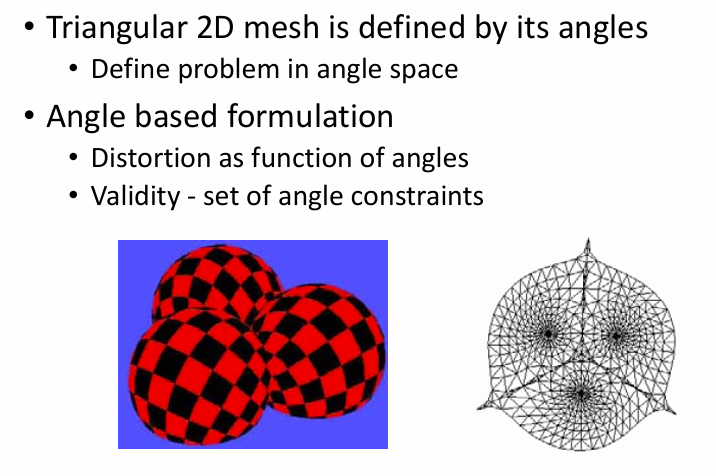
Angle Based Flattening (ABF) & ABF++:3D模型表面参数化的算法,它通过最小化角度失真来生成低失真的参数化结果。
As‐rigid‐as‐possible (ARAP) :3D模型表面参数化的算法,其核心思想是在保持局部区域尽可能刚性的同时,通过全局优化实现整体形状的变形。特别适用于需要保持模型局部细节的场合。

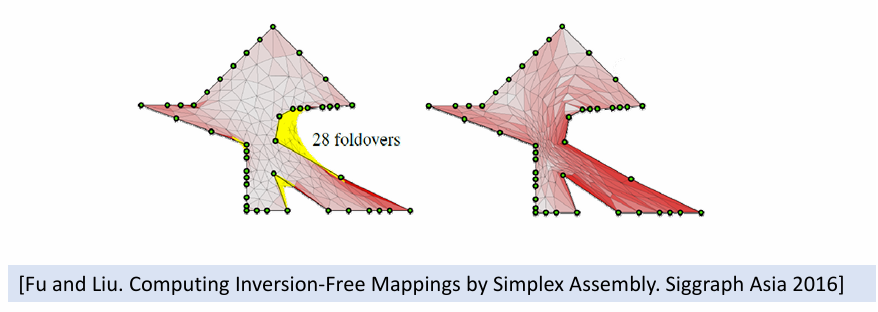
Simplex Assembly:计算无翻转(inversion-free)映射的方法,它在保持低失真或有界失真的情况下,对单纯形网格进行处理。(单纯形分解(simplex disassembly)和单纯形组装(simplex assembly))
Bijective Parameterizations
一种在几何处理和计算机图形学中用于3D模型表面参数化的技术,其目标是创建一个全局单射(one-to-one)的映射,确保参数化过程中没有翻转或自我相交。
- Quasi‐Newton (QN)
- Scaffold
- Efficient Bijective Parameterizations
封闭曲面的割缝问题
一个封闭的表面不能被展平,需要一个切口将其切开成一个类似圆盘的区域。
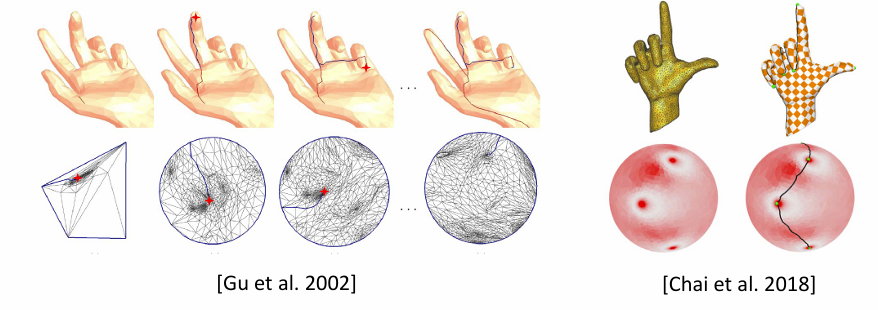
最小生成树方法(Minimum Spanning Tree, MST):
- 节点选择:在最小生成树方法中,节点(或顶点)通常选择具有高曲率或高失真的极值点。这些点在参数化过程中对于保持模型的细节和特征至关重要。
- 最小生成树构建:构建一个图的最小生成树,该树连接所有选定的节点,且总边权重最小。在表面参数化的上下文中,边权重可以基于多种因素,如距离、角度失真或面积失真。
- 展平策略:一旦构建了最小生成树,就可以使用它来指导表面展平的过程。一种常见的策略是将最小生成树的叶子节点(没有子节点的节点)展平,然后逐步向中心节点推进。
- 减少失真:通过在最小生成树的基础上进行展平,可以减少全局失真,因为最小生成树倾向于保持局部结构的完整性。
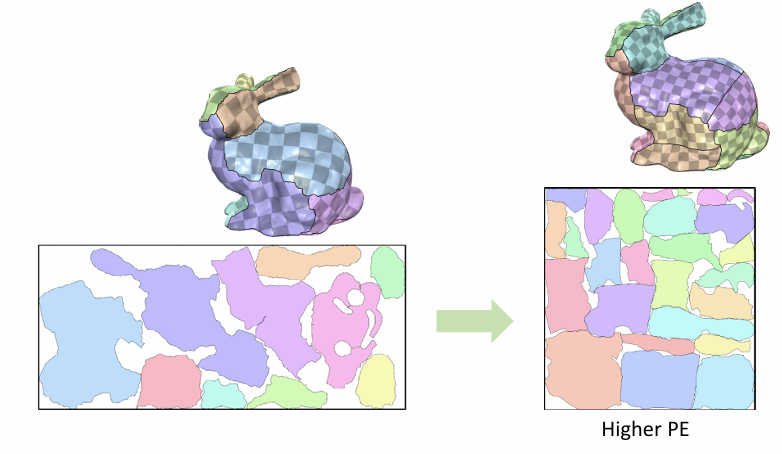
纹理地图:多片参数化
多片参数化是一种纹理地图技术,它将模型表面分割成多个小片,每一片单独进行参数化,以减少单个参数化过程中的失真。
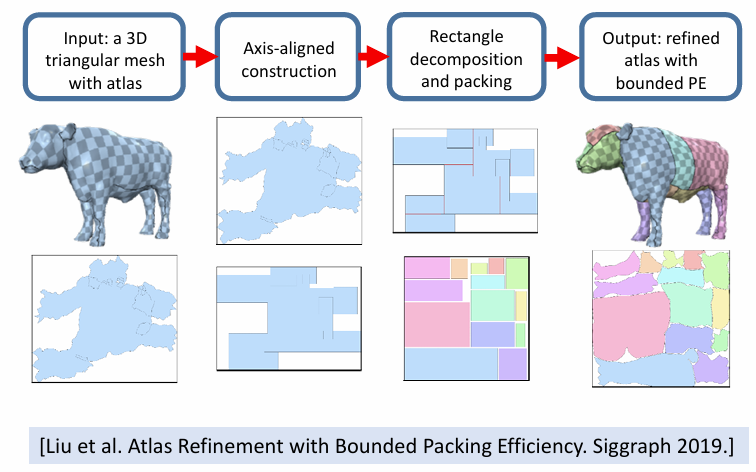
Atlas Generation(图集生成)是一个关键过程,它涉及到将模型表面分割成多个图表(charts),并将这些图表展平成2D区域。Minimizing Packing Efficiency (PE) 是图集生成中的一个核心问题,它指的是在将这些2D图表紧凑地排列到一个矩形区域中时,如何最大化空间利用率,即最小化未使用的空间。
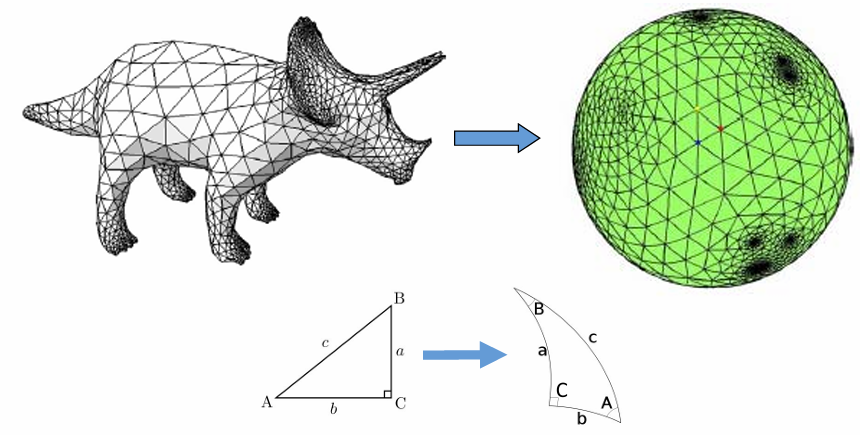
球面参数化
输入:亏格为0的封闭曲面(拓扑同胚于球面)
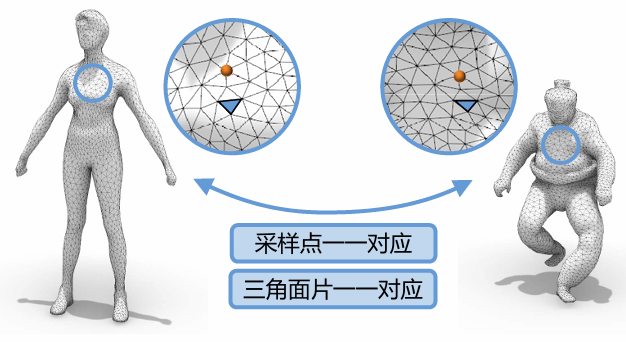
Mapping between Mesh Surfaces:将一个3D模型的表面映射到另一个模型表面或者从模型表面映射到一个参数域。
相容性网格(Compatible mesh):一组具有相同连接关系且与给定模型形状近似的网格
总结:曲面参数化
- 是一个从3D到2D的降维问题:将几何数据表达为图像
- Next: 大型场景的压缩、传输、调度、渲染…

曲面简化
大规模网格数据在存储、传输、处理、渲染方面都存在着挑战。
冗余数据:信息熵
在不损失视觉效果的情况下减少数据量
考量因素:Level of details (LOD)
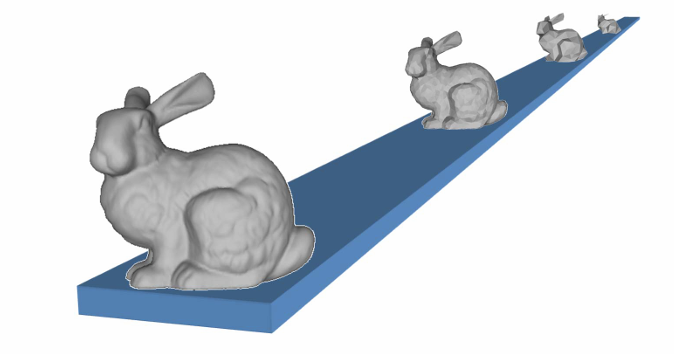
曲面简化例子:
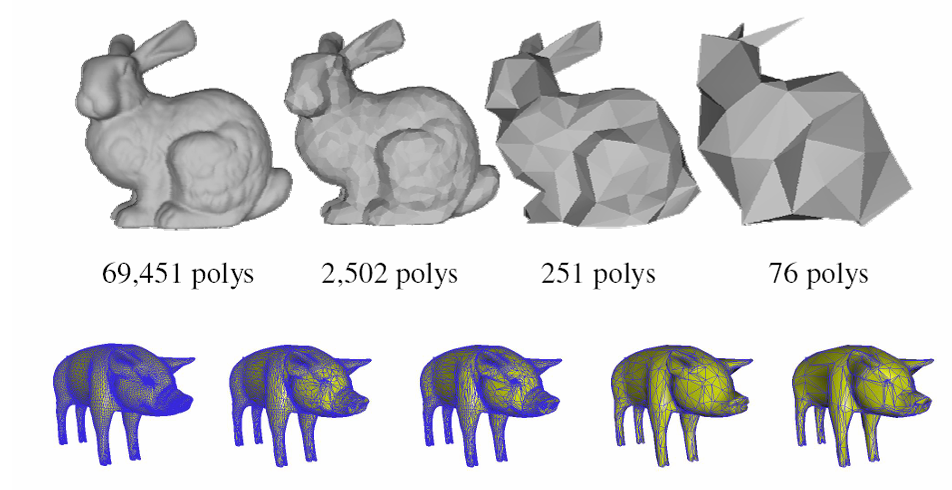
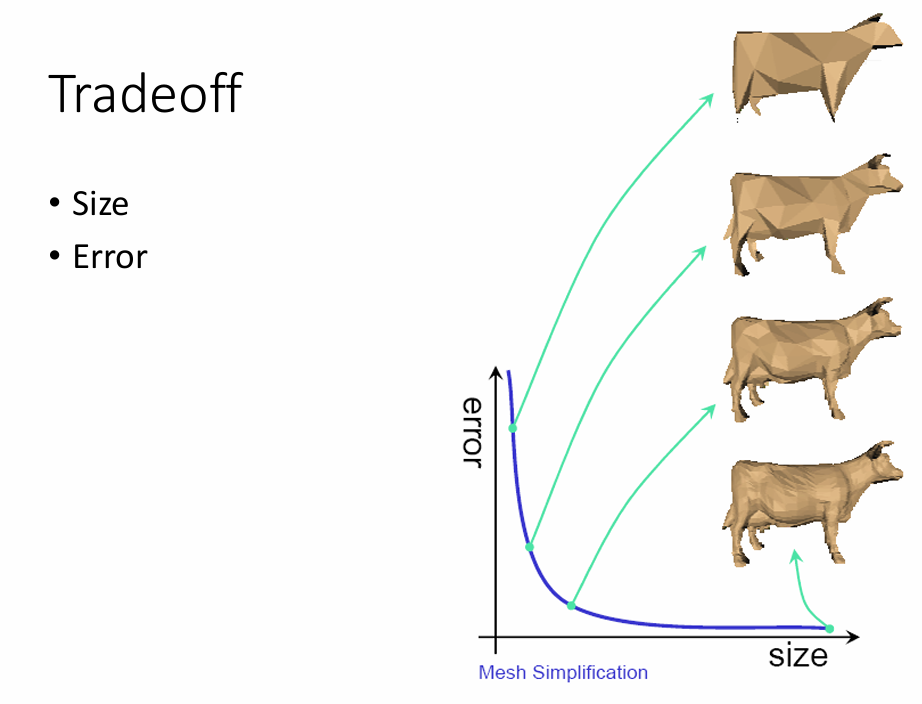
简化方法:
- 几何对象:
- 顶点
- 边
- 面
- 简化度量:
- 几何
- 视觉:纹理、材质、法向……
简化流程:
- 一系列局部操作
- 涉及邻近邻居 - 每次操作只影响小范围区域
- 每次操作都会引入错误
- 寻找并应用引入最小错误的操作
简化方法:
- 去除点
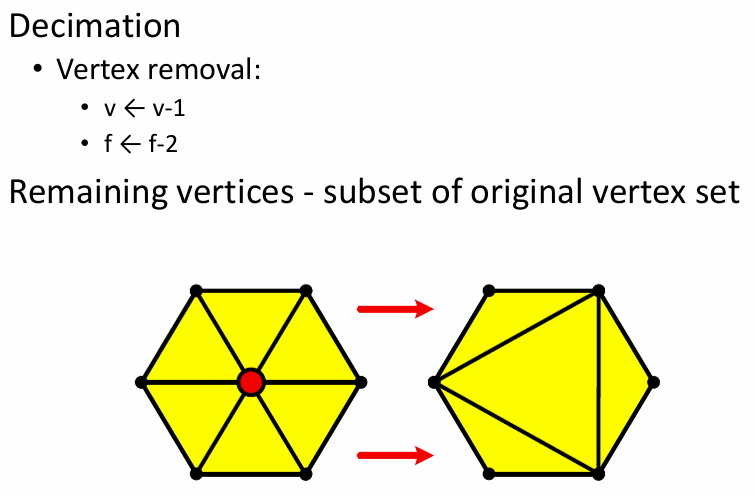
- 减少边:
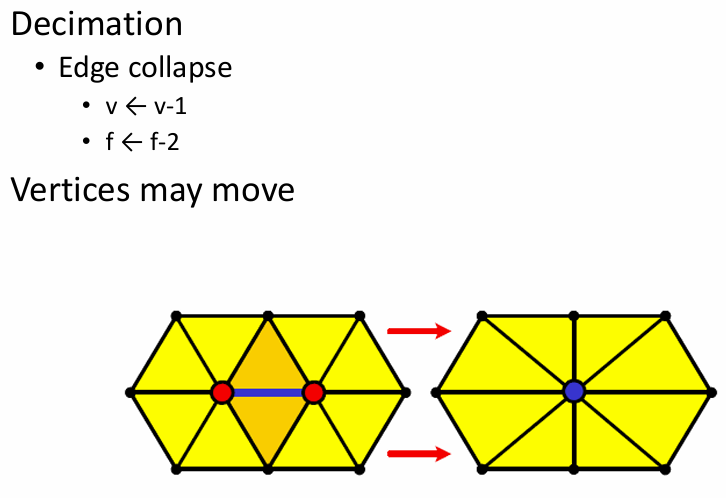
- 减少三角形
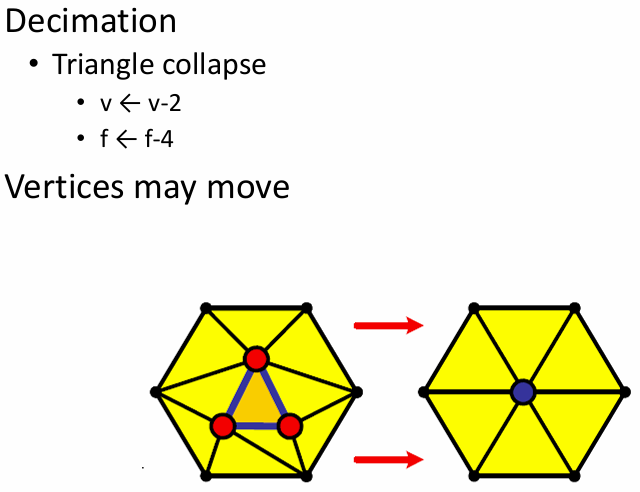
- 顶点聚合
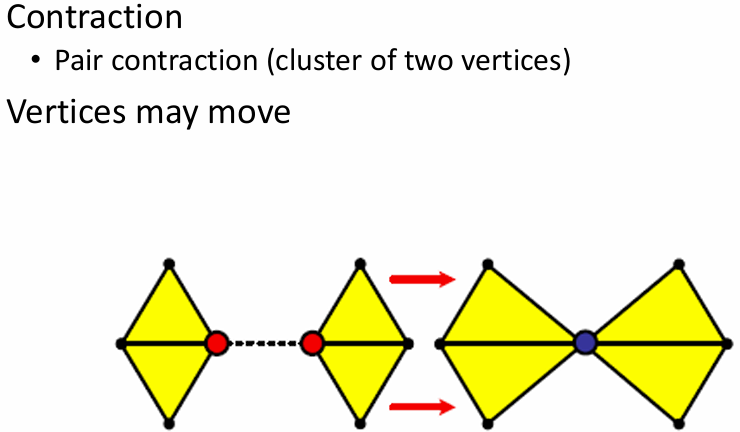
- 顶点集聚合
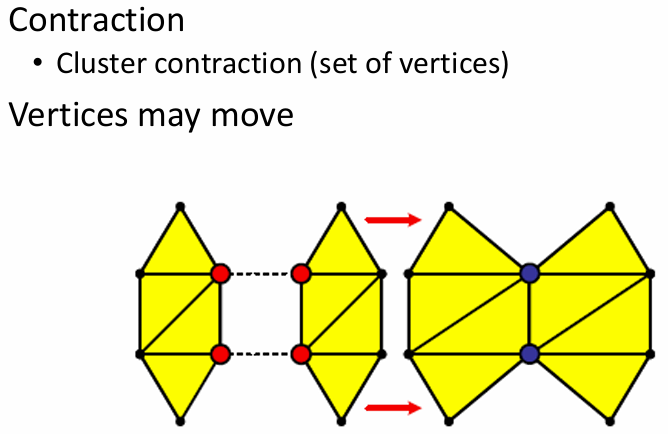
- 顶点聚类
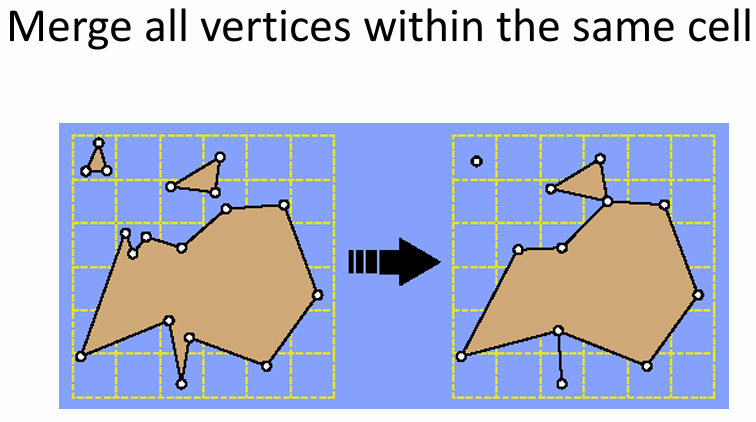
Error Control:
- 局部错误:将新区域与前一次迭代进行比较
- 快速
- 累积错误
- 不占用内存
- 全局错误:将新区域与原始网格进行比较
- 慢速
- 更好的质量控制
- 可以用作终止条件
- 必须在整个算法过程中记住原始网格
局部简化策略:重复执行以下步骤
- 选择误差最小的元素。
- 执行简化操作(移除/收缩)。
- 更新误差(局部/全局)。
- 直到达到所需的网格大小/质量。
度量标准:
- 平面距离(Distance to plane):简化后的面与原始面之间的距离。
- 曲率(Curvature):简化对模型表面曲率的影响。
- 通常使用近似方法来计算这些度量。
- 平均平面(Average plane):用于近似计算的平面。
- 离散曲率(Discrete curvature):使用公式 Σa/2πΣa/2π 来计算,其中 aa 代表围绕顶点的角度总和。
全局简化策略:
Mesh Re-tiling(网格重铺):
- 目标:通过引入新的“非均匀分布”的顶点来简化和改善网格。
- 方法:重铺尝试在保持网格整体结构的同时,减少顶点数量并优化网格质量。
Mesh Optimization(网格优化):
框架:将简化过程视为一个优化问题
能量函数:最小化某个能量函数
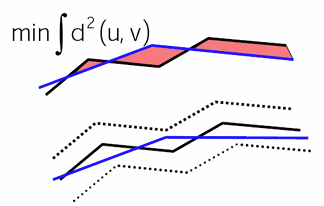
评估:在改变前后评估,接受那些降低能量的更改
Level of Detail (LOD)
多分辨率表示:
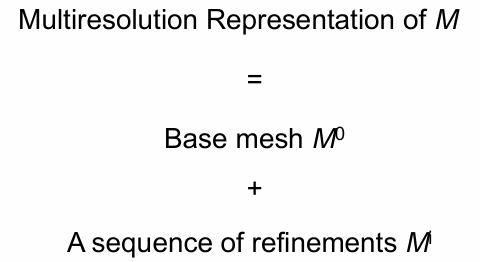
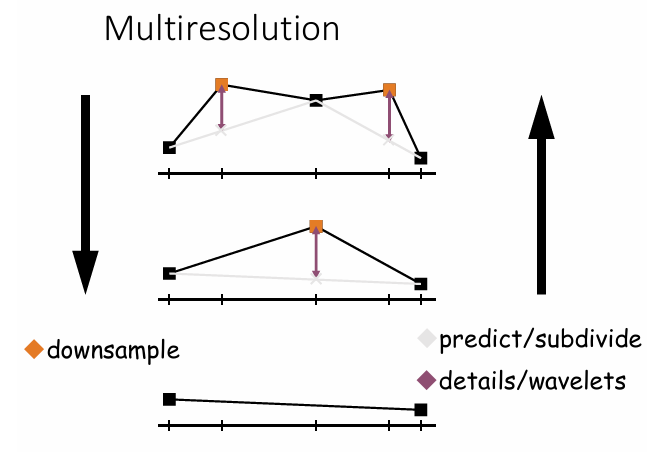
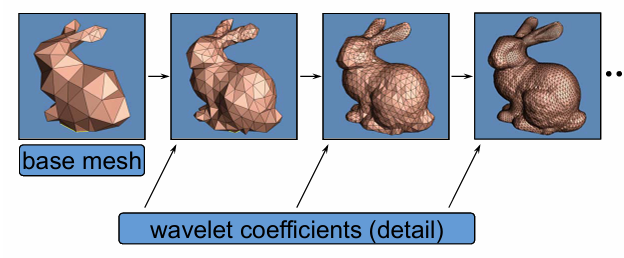
离散LOD:
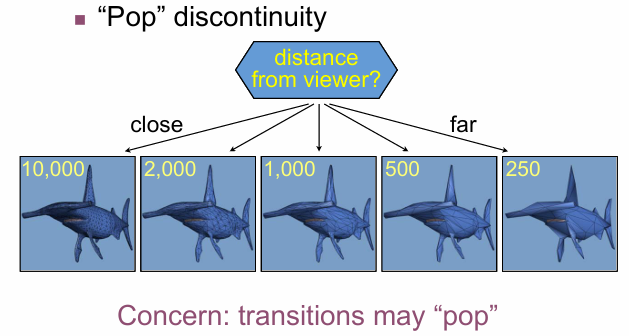
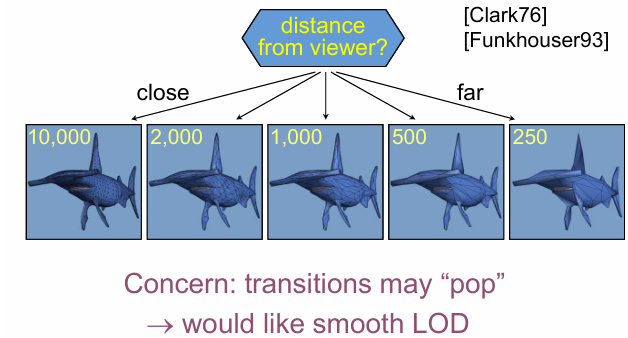
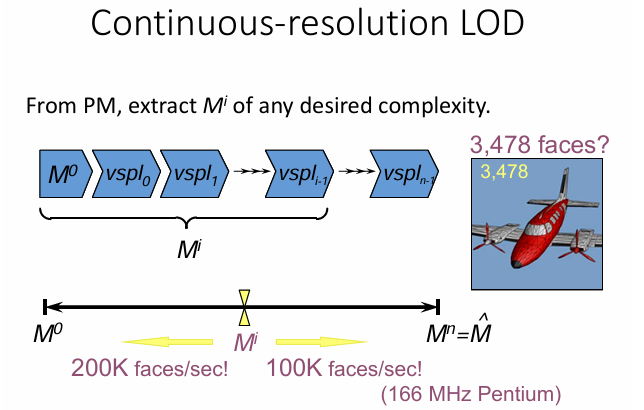
连续LOD:
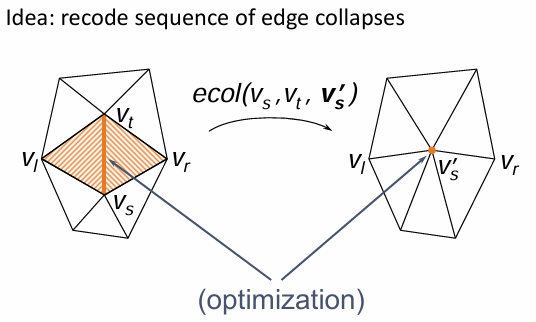
网格简化过程:
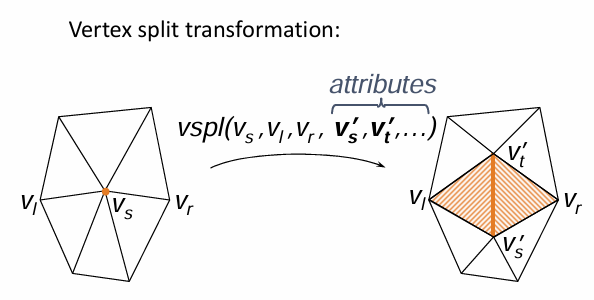
反向:
View‐Dependent LOD 基于视景的LOD:以比远处部分更高的分辨率显示物体附近的部分。