Lecture 10 Surface Denoising & Sampling & Spliting
曲面去噪
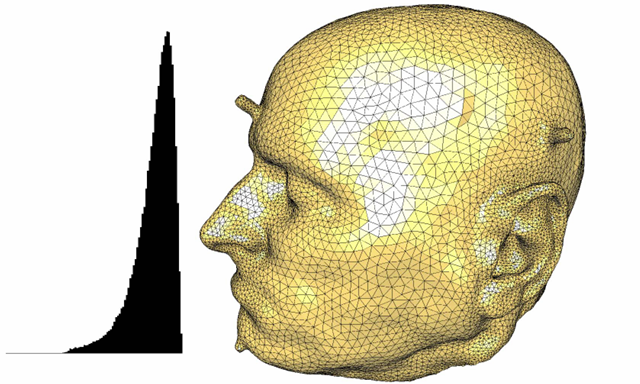
网格曲面上的噪声:Meshes obtained from real world objects are often noisy.

噪声常见形式:

光滑/去噪问题:
- 输入:M(含噪声的网格曲面)
- 输出:M0(无噪声的网格曲面)
- 去噪模型:
- M = M0 + ε
- Challenge:等式右边的两个参数都不可知
Mesh smoothing:
- 假定:网格顶点的数据及连接关系不变
- 问题转化为:求顶点的新位置(顶点偏移的方向),使得“噪声”减少
- 对顶点进行适当的扰动或偏移
Mesh Smoothing Problem:
- 输入:M(含噪声的网格曲面)
- 输出:M0(无噪声的网格曲面)
- 网格去噪模型:
- 𝒗 = 𝒗0 + εn(∀𝒗 ∈ M)
- Challenge:顶点的位移 n 是多少
- The normal of 𝒗 : doable → 新模型
- 𝒗0 = 𝒗 − εn
- 若干次迭代找无噪声模型(反向求解)
滤波:
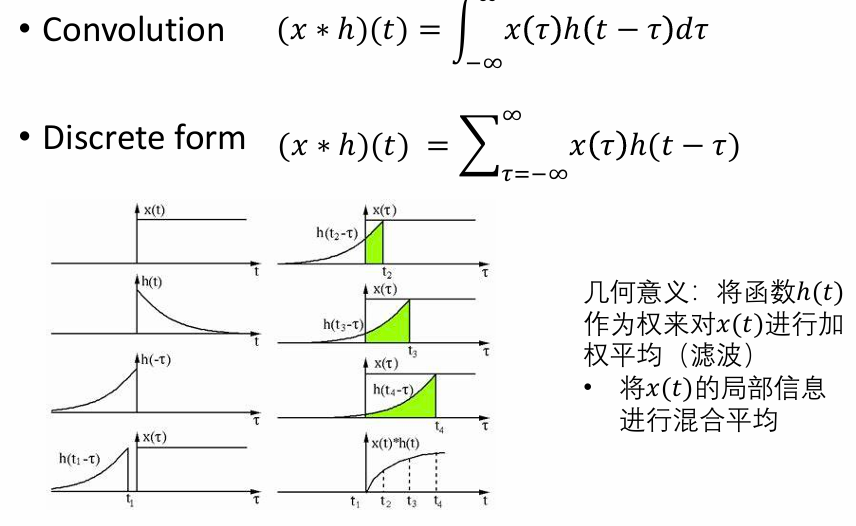
顶点滤波
拉普拉斯光滑
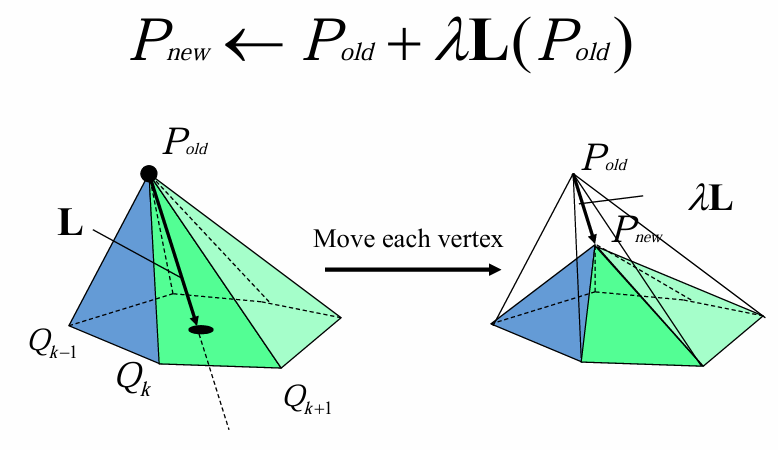
平均曲率流
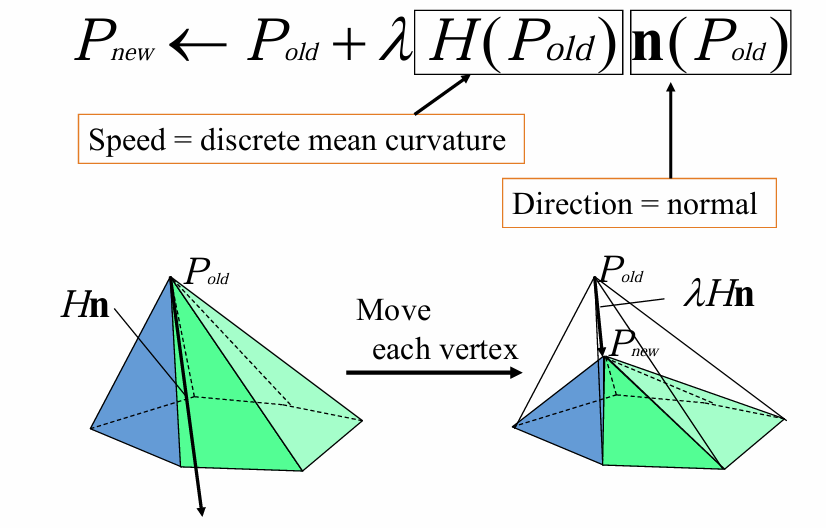
双边滤波

隐式网格演化

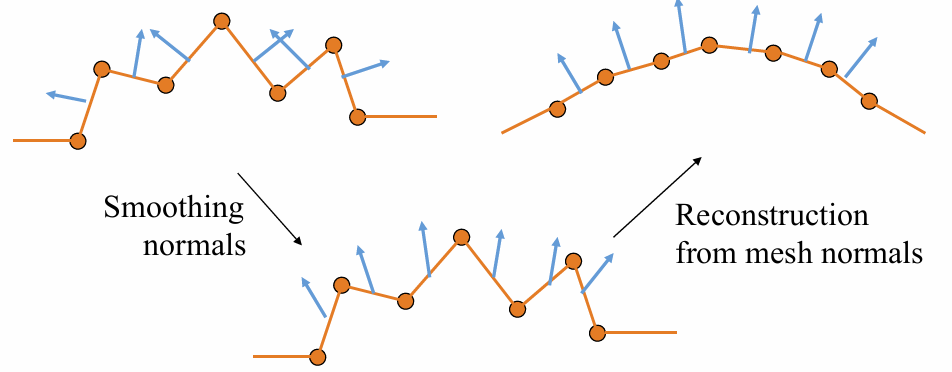
法向滤波
- 先对法向进行滤波:可使用顶点滤波的任何方法
- 根据滤波后的法向重建网格顶点
- 输入:滤波后的法向量场
- 输出:重建网格顶点,使得其法向量接近输入
- 优化方法:求解线性方程组
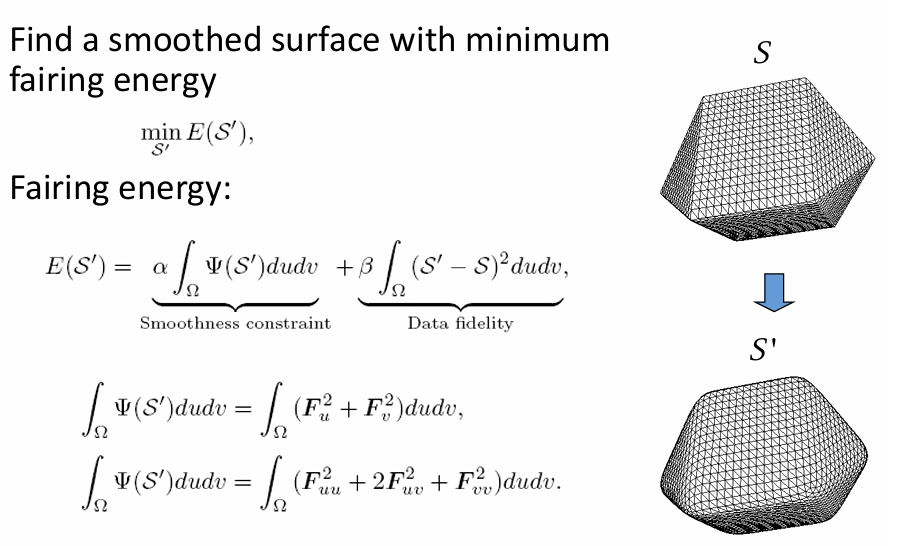
全局光滑
全局光滑方程组(和上节课的全局拉普拉斯光滑一样)
网格改进(Mesh Improvement)
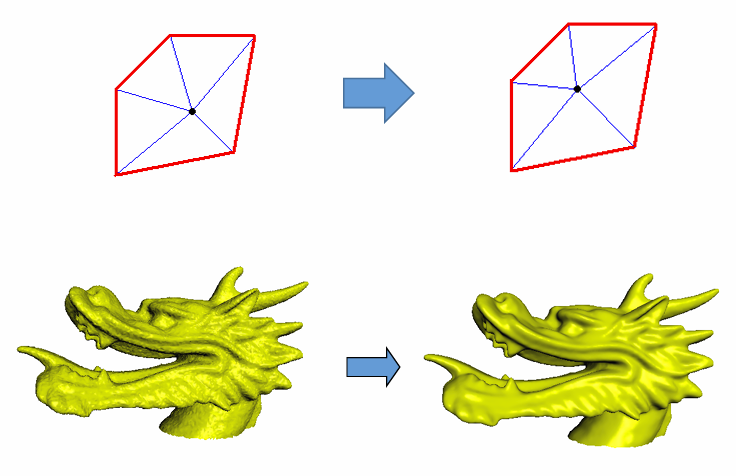
改进网格质量:
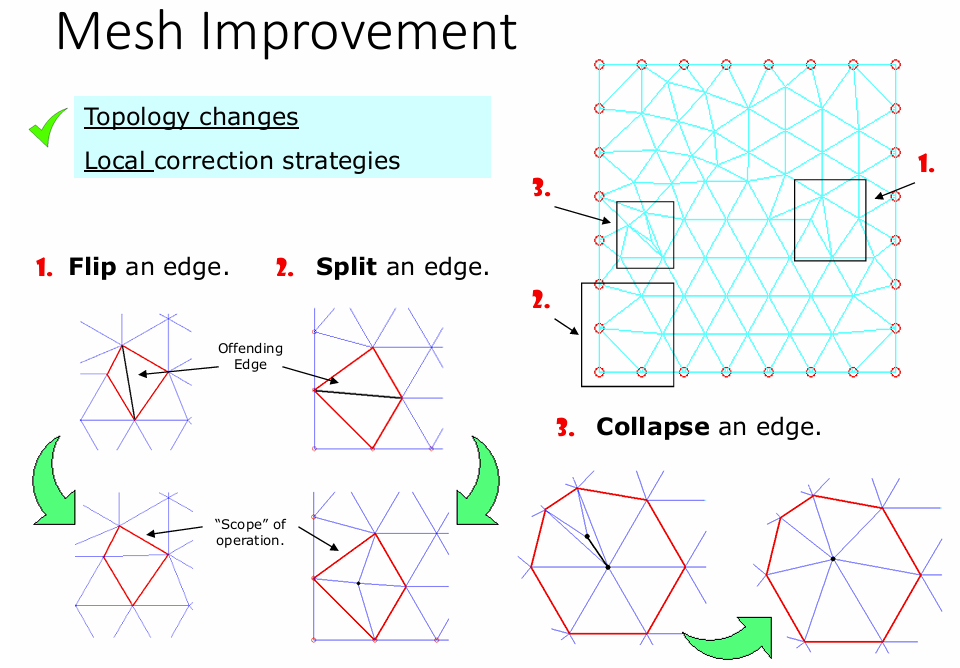
其他去噪方法:
- 基于稀疏优化的方法
- 基于压缩感知的方法
- 基于机器学习的方法
- ……
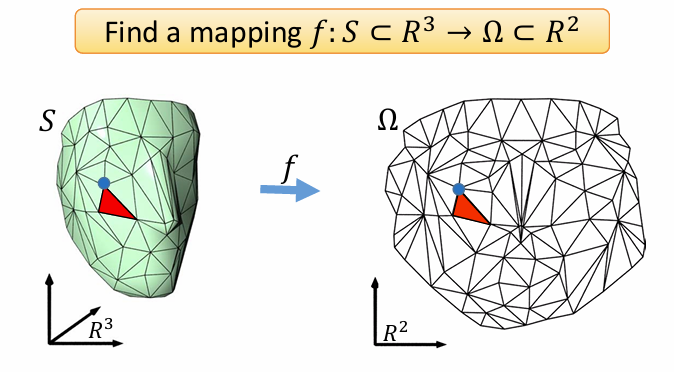
采样(Sampling)
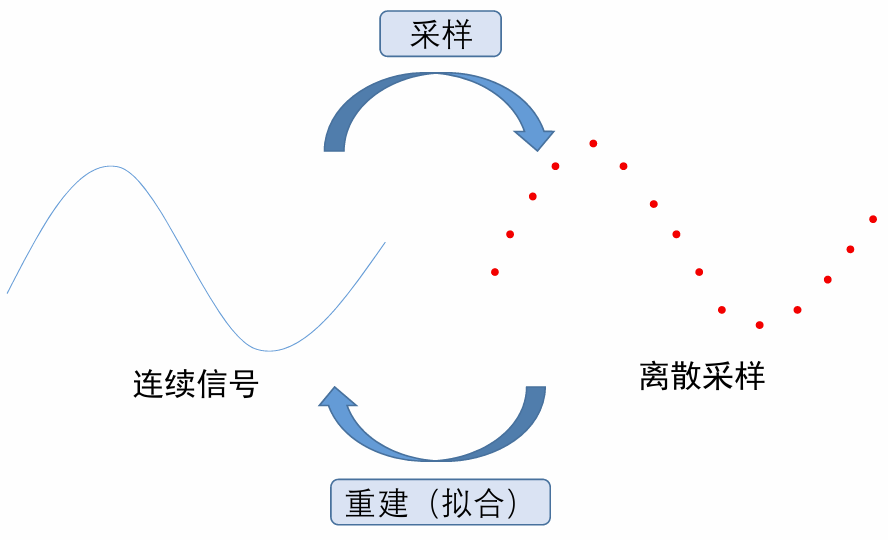
采样:从连续到离散
曲线曲面的离散表达
曲线的绘制:
GDI/OpenGL 绘制基本单元:点、线段
曲线须离散成多边形
曲面的绘制:
- OpenGL 绘制基本单元:点、线、三角形
- 曲面须离散成三角形网格
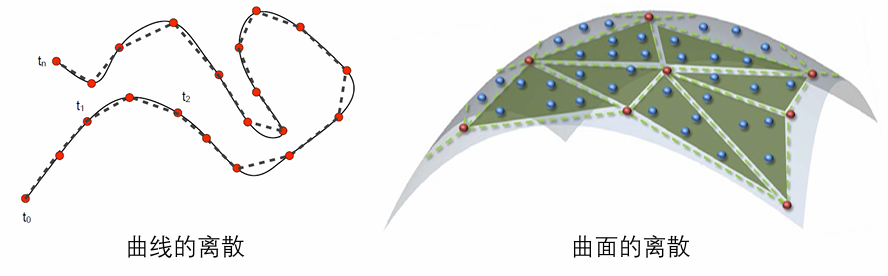
离散的本质:采样(Sampling)
- 曲线曲面的采样
- 在参数域上采样
- 直接在原始曲线曲面采样
- NURBS曲线曲面的采样误差估计
- 可进行理论上的误差分析
- 逆向工程:
- 采样点的获取
- 通过扫描硬件设备得到采样点
- 通过(多视点几何)重建算法计算得到采样点
- 重建问题:如何通过采样点重构原始曲线/曲面
- 连续重建:用连续函数来拟合表达
- 离散重建:直接得到离散基元表达
- 采样点的获取
- 图像:区域的采样
- 视频:时间的采样
采样与重建:
欠采样产生频率的走样:
- 高频函数拟合低频信号:过拟合
- 低频函数拟合高频信号:欠拟合
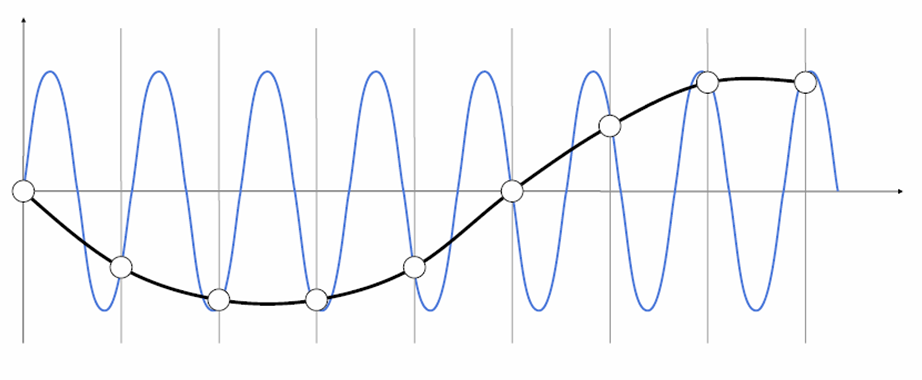
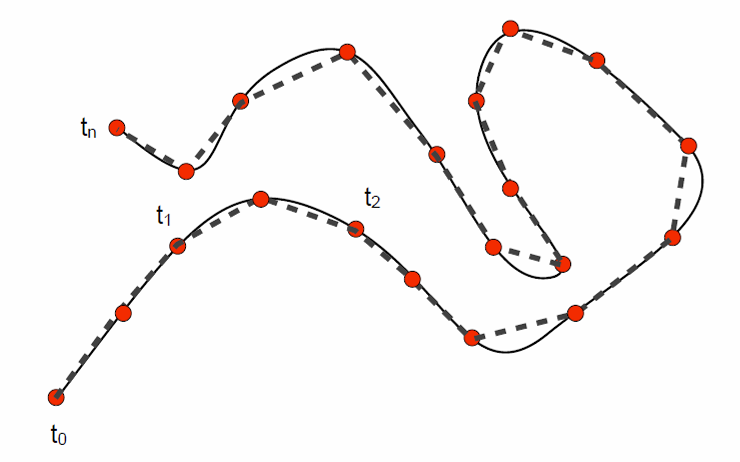
1D曲线的采样:分段线性逼近表达
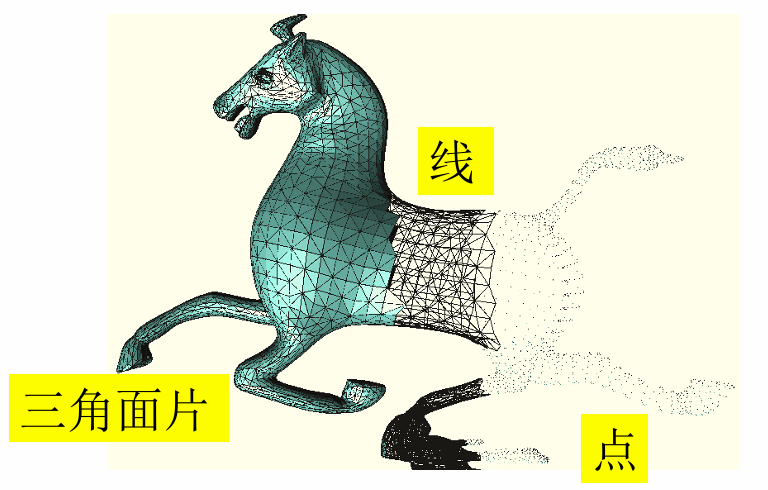
2D曲面的采样:分片线性逼近表达
平面规则区域的采样:将一个区域分解为若干个小区域

平面区域的不规则采样:将一个区域分解为若干个小区域
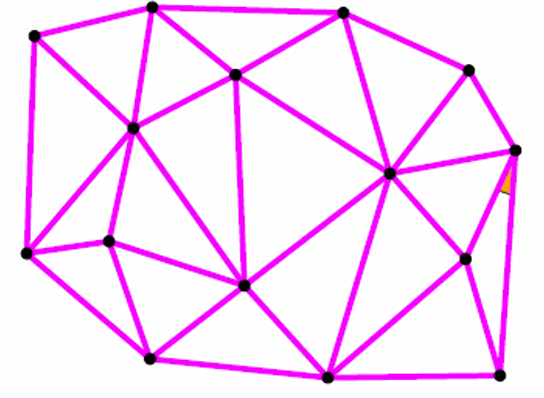
Triangulation(三角剖分): 复杂函数的分片线性逼近(piece‐wise linear approximation)
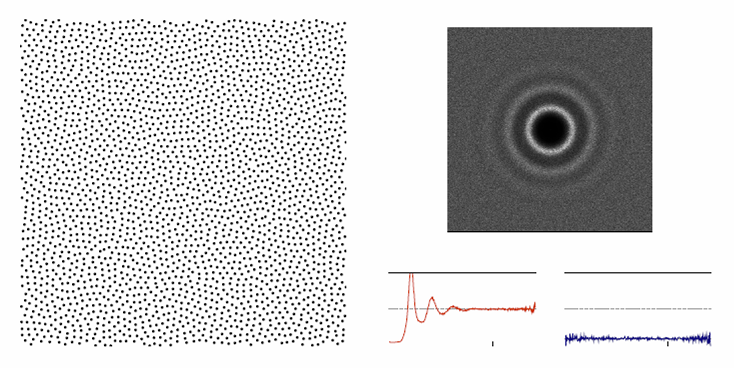
Blue Noise Sampling(蓝噪声采样):看着均匀但不规整
- (左)均匀分布但随机定位的点集
- (右)蓝噪声分布的典型功率谱、径向平均功率谱和各向异性
平面三角网格
给定平面上一些点,如何生成比较好的三角剖分(一般认为左边比右边好)
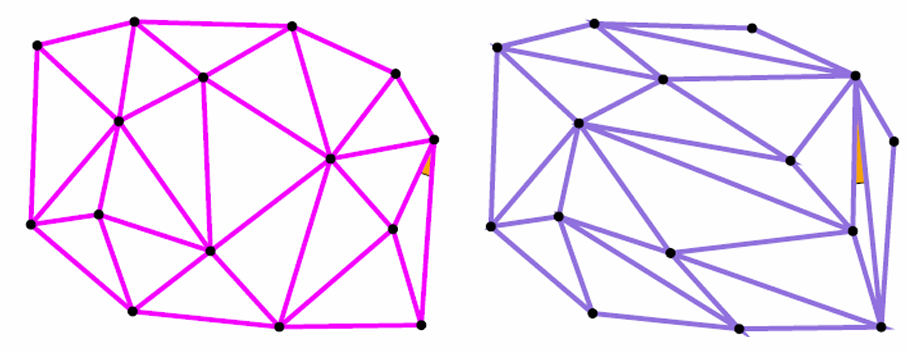
衡量网格质量的标准有很多标准:
- 最小角度(Minimal angle):网格中所有角度的最小值,较大的最小角度通常意味着网格质量较好。
- 平均比率(Mean ratio):可能指的是网格中元素形状的一致性,例如在三角形网格中,这可能与三角形的边长比有关。
- 纵横比/半径比(Aspect/radius ratio):衡量网格元素的长宽比,较低的纵横比通常表示更好的网格质量。
- 奇异值(Singular values):在数值分析中,奇异值可以用于评估矩阵的条件数,进而反映网格的质量。
定义一个被所有人接受的通用网格质量标准并不容易,但普遍认为最好的简单形是等边三角形和正四面体。这些形状在几何上是对称的,具有均匀的属性,因此在许多应用中被认为是最优的网格元素。
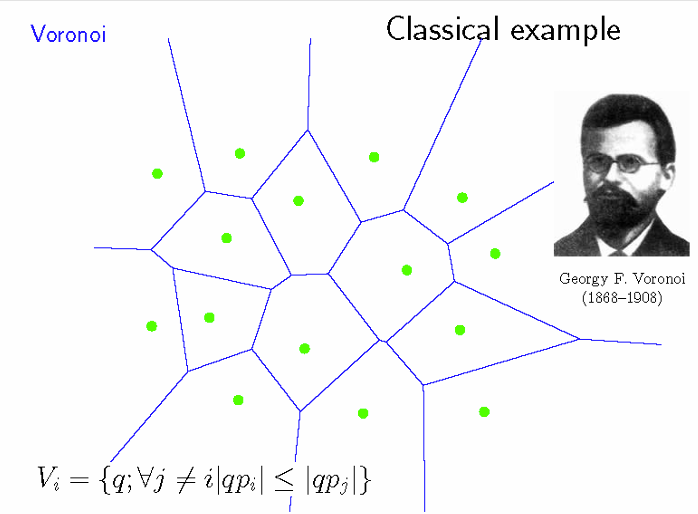
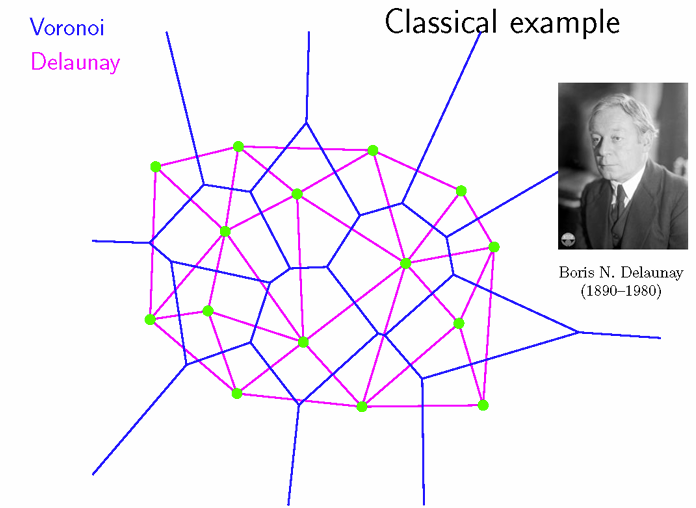
Delaunay三角化
Voroni图:所有边都是由某两个点的中垂线组成
Delaunay三角化:Voroni图对偶过来,由点去构成三角形
网格剖分(Mesh Generation)
DT (Delaunay Triangulation,德劳内三角剖分)只在点固定时优化连接,但点的分布对于一个好的网格来说更为重要。

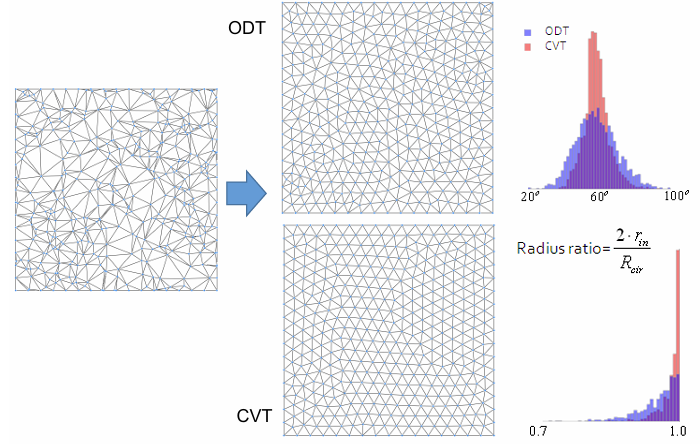
优化网格的方法:CVT(Centroidal Voronoi Tessellation, 质心Voronoi镶嵌)
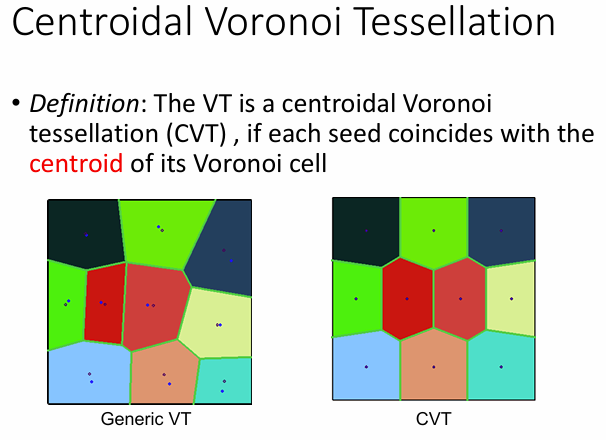
定义:当每个种子点(seed)与其Voronoi单元(Voronoi cell)的质心(centroid)重合时,这种Voronoi镶嵌被称为质心Voronoi镶嵌(CVT)。
图示:
- 左图(Generic VT):普通的Voronoi镶嵌,其中种子点(紫色点)随机分布,每个种子点周围的多边形区域是该种子点的Voronoi单元,即所有距离该种子点最近的点的集合。
- 右图(CVT):质心Voronoi镶嵌,其中每个种子点都位于其Voronoi单元的质心位置。这种布局使得Voronoi单元的形状更加均匀,种子点的分布也更加平衡。
CVT迭代方法:Lloyd算法
构建Voronoi镶嵌(VT):首先,根据给定的点集构建Voronoi镶嵌。每个点都会生成一个Voronoi单元,该单元包含所有距离该点比其他点更近的点。
计算Voronoi区域的质心:对于每个Voronoi单元,计算其质心,即该单元内所有点的平均位置。
将点移动到质心:将原始点移动到其对应Voronoi单元的质心位置。
迭代直到收敛:重复上述步骤,直到点的位置不再发生显著变化,即算法收敛。收敛意味着点的分布已经达到了一个稳定状态,此时的Voronoi镶嵌即为质心Voronoi镶嵌。
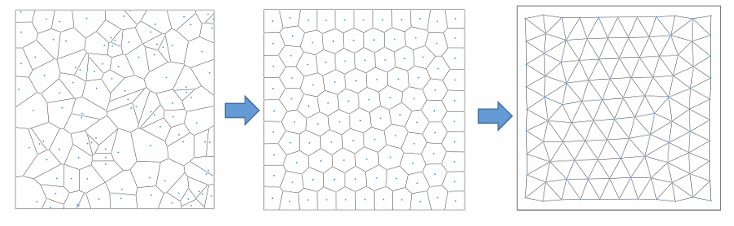
Optimal Delaunay Triangulation (ODT):一种特殊的Delaunay三角剖分,它在所有具有相同顶点数的三角剖分中,最小化了插值误差。
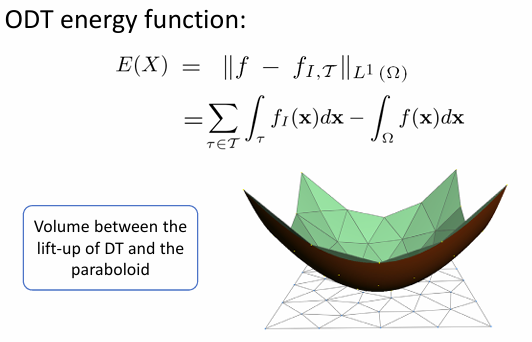
CVT & ODT Energy:
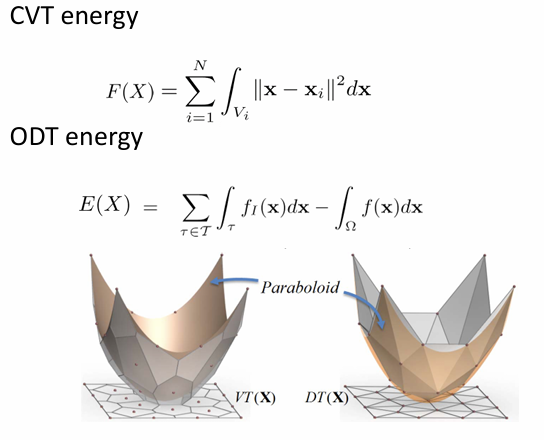
Compare ODT and CVT:
高维几何对象的采样与剖分
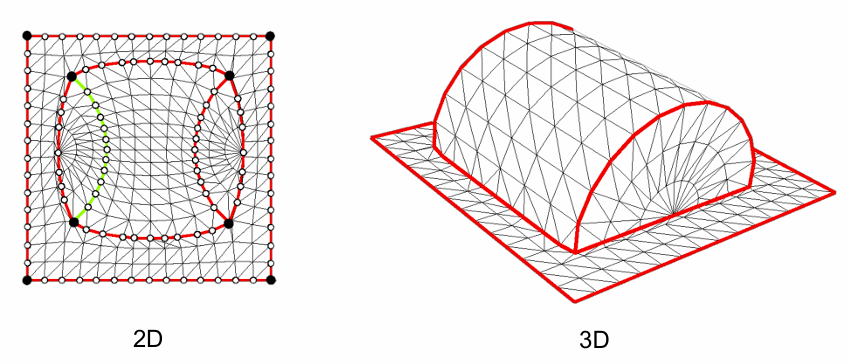
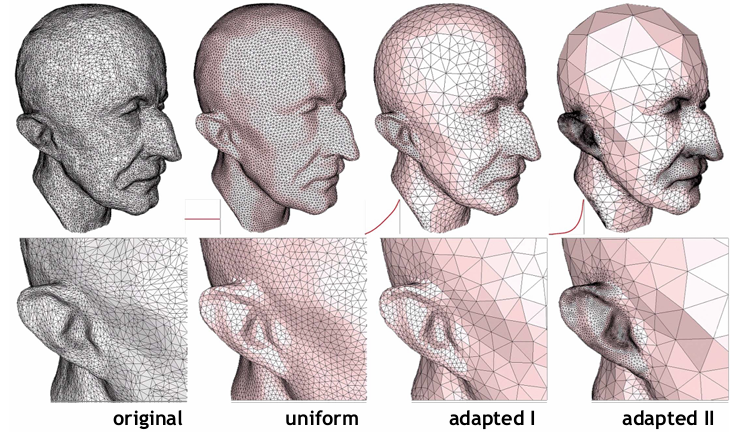
二维流形曲面的采样与网格化:
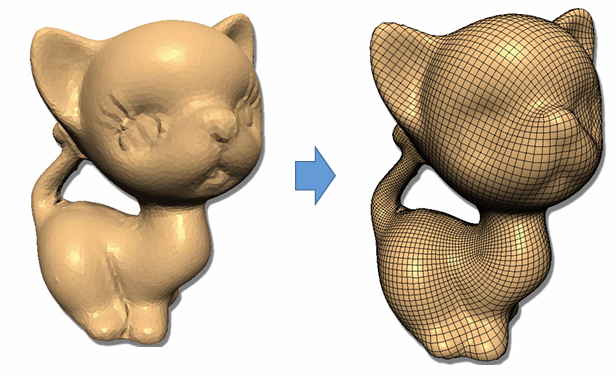
二维流形曲面的四边形网格化:
空间体的采样与剖分:
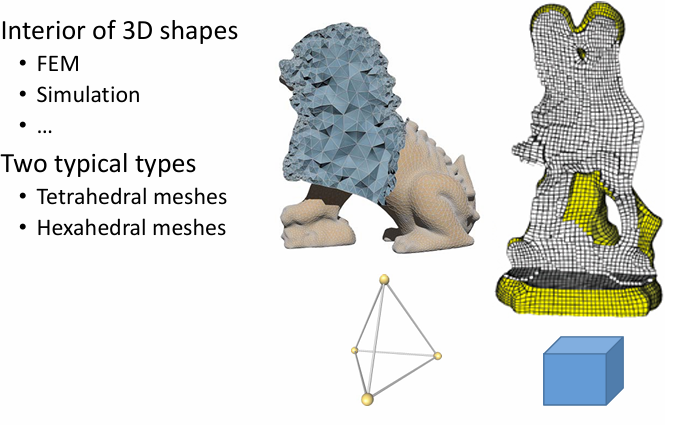
空间体的四面体网格: