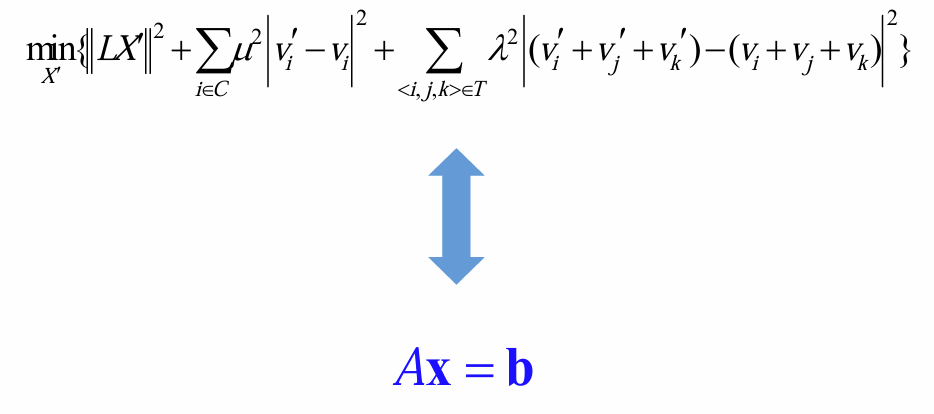GAMES102-09-微分坐标

Lecture 09 Differential Coordinate

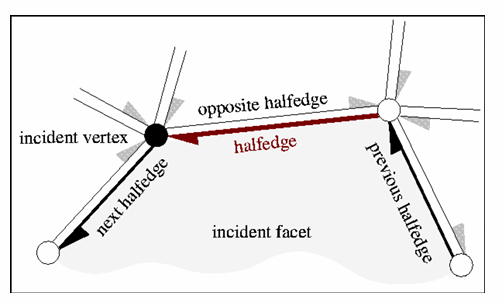
局部特征度量：1‐邻域

• 一般“流形”结构也是通过局部邻域来定义

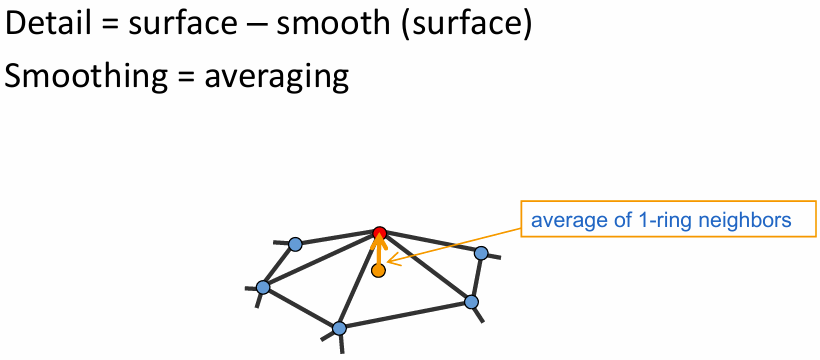
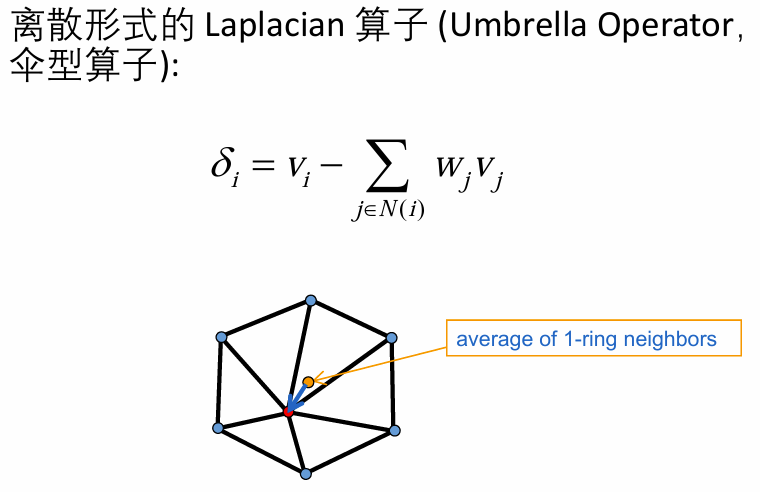
Laplace算子(operator)：

Differential Coordinates （微分坐标）：直观上感觉就是橙色点（附近点平均值）和红色点（实际值）的距离

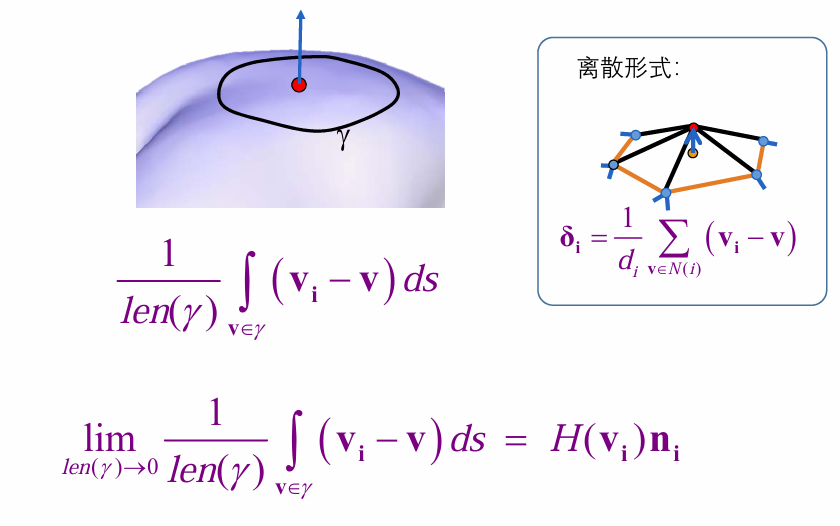
平均曲率流定理：

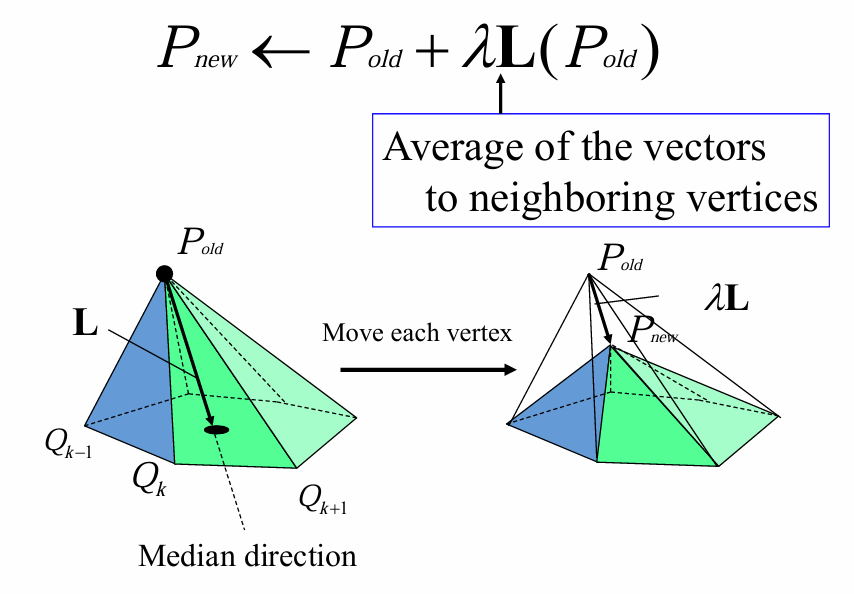
拉普拉斯光滑：

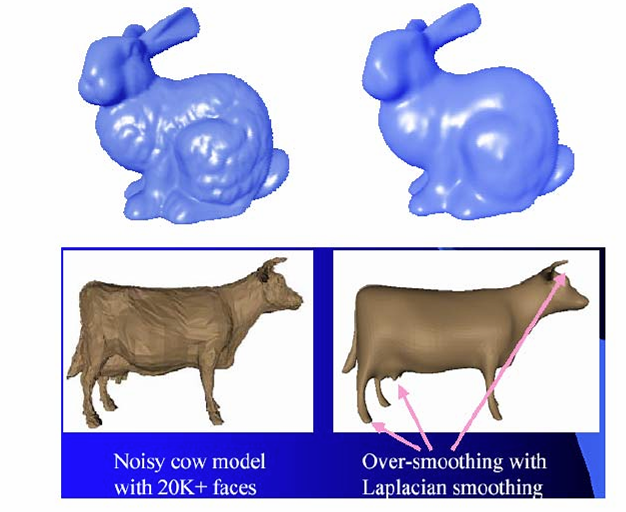
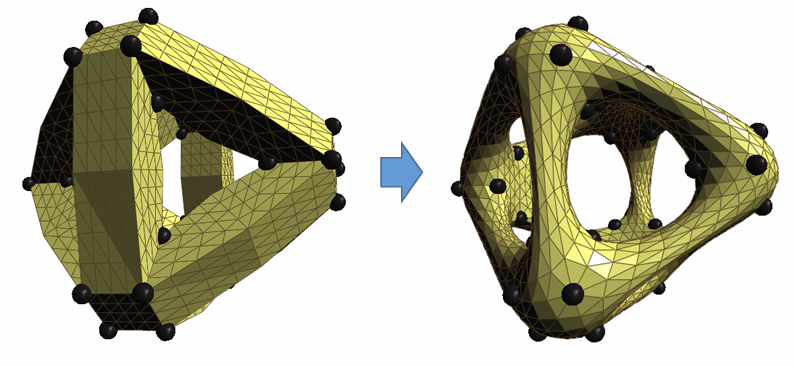
拉普拉斯光滑例子：有可能会丢掉细节（over smoothing）

Global Laplacian Smoothing（全局拉普拉斯光滑）

局部迭代光顺方法的问题：

• 迭代时有些地方快、有些地方慢
• 有些地方的结果会产生自交

同时满足微分坐标为0

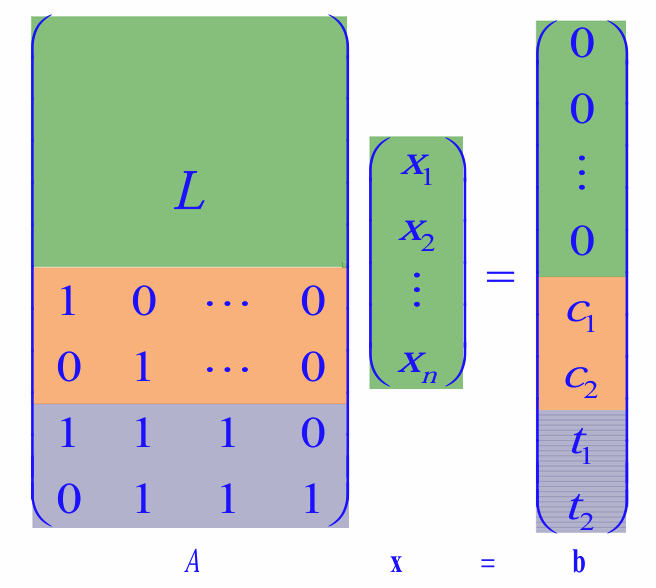
A是n×n的矩阵，但非常稀疏

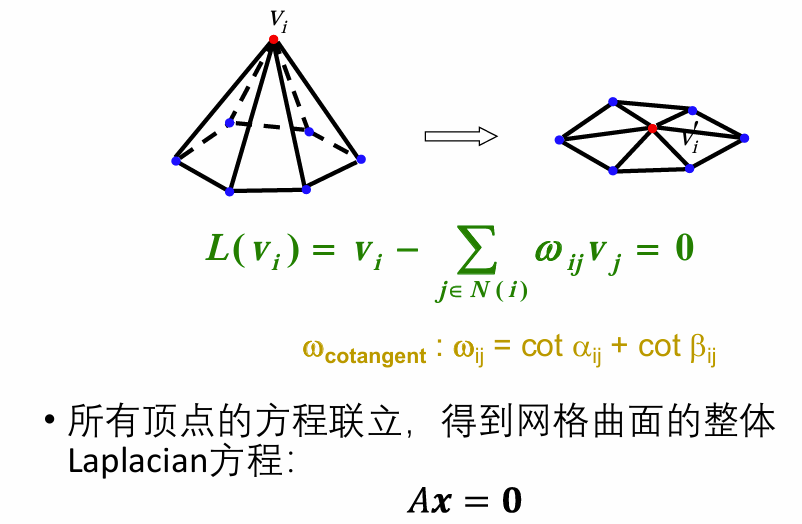
拉普拉斯矩阵：

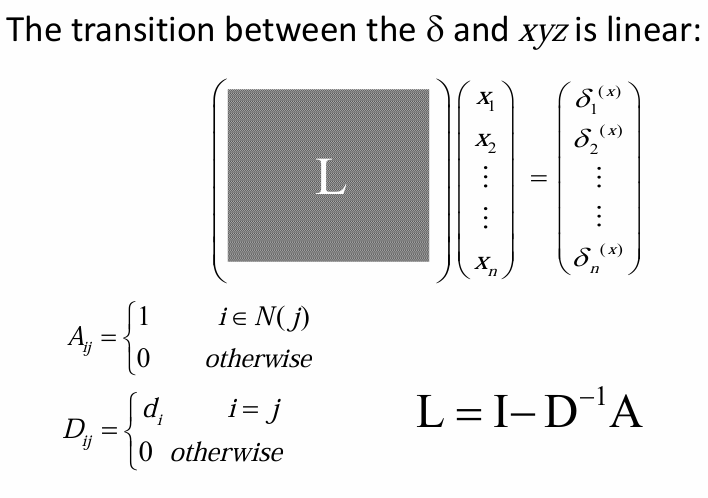
极小曲面生成的全局方法：

• 检测边界，固定边界
• 构建稀疏方程组
• 求解稀疏方程组
• 更新内部顶点坐标

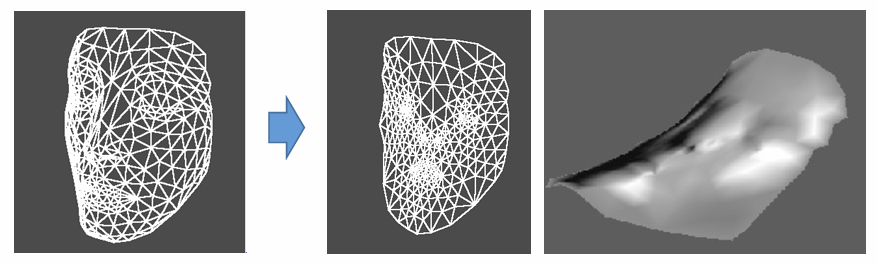
曲面参数化

参数化：将曲面展开成平面

每个3D顶点(x,y,z)对应一个2D点(u,v)

• (u,v) 称为 (x,y,z) 的参数（2D流形曲面的本征维数）

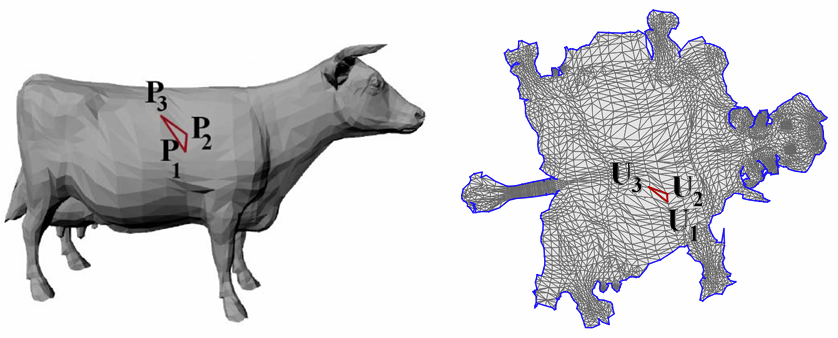
参数化是几何处理中的基本问题

• 提供了三维曲面每个点的一个二维参数
  • 本征维数参数
• 在低维来处理高维问题，减少复杂度
  • 降维
• 三维曲面之间的相关问题可通过参数化空间来处理

基本方法：将边界映射到平面的凸多边形上

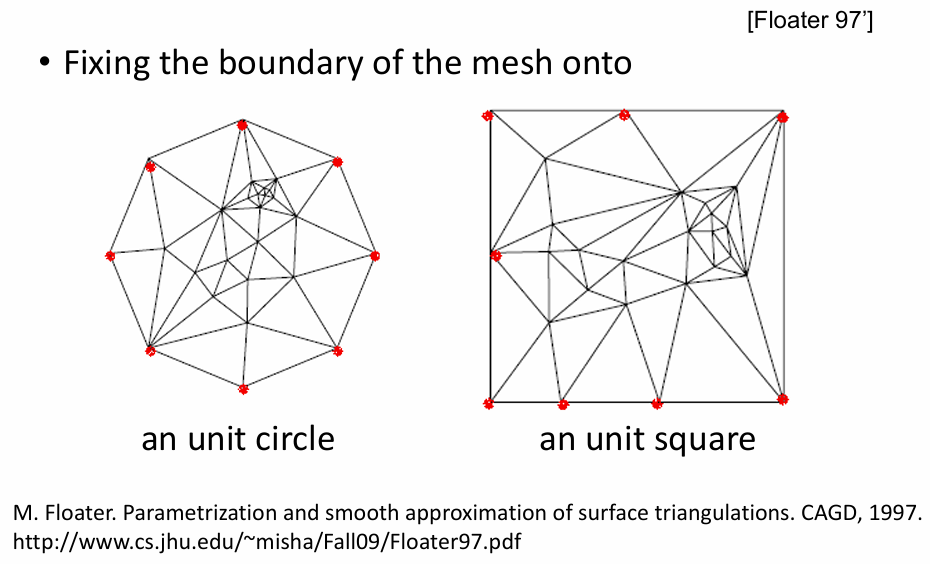
可以证明：如果边界位于凸多边形上，则三角形一定不会发生翻转

参数化操作步骤：

• 检测边界
• 将边界映射到正方形边界或圆边界（凸边界）
• 构建稀疏方程组
• 求解稀疏方程组
• 更新顶点坐标
• 连接纹理图像，更新显示

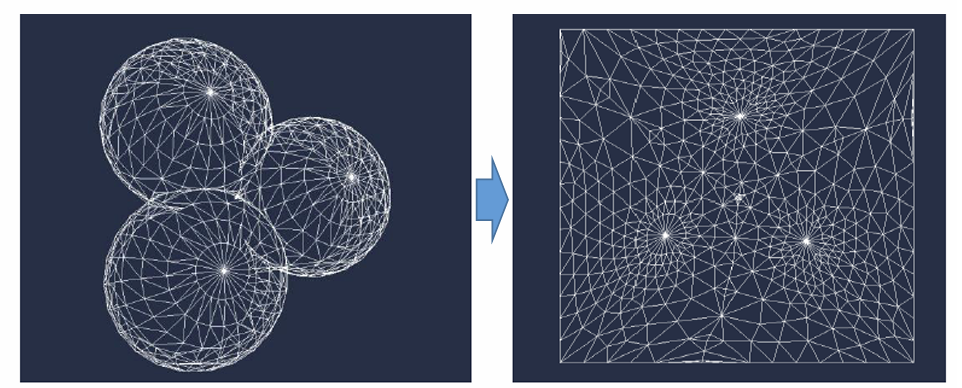
曲面展开（参数化）：

纹理映射：

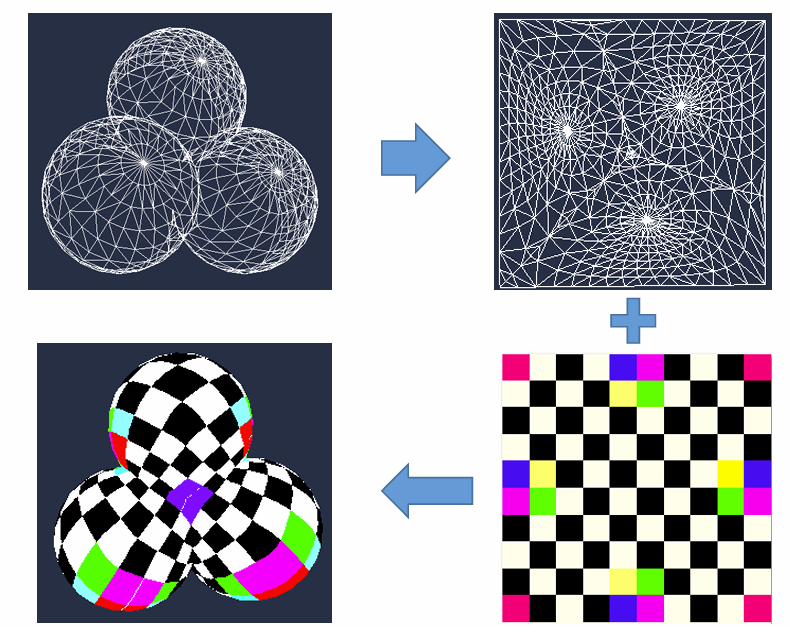
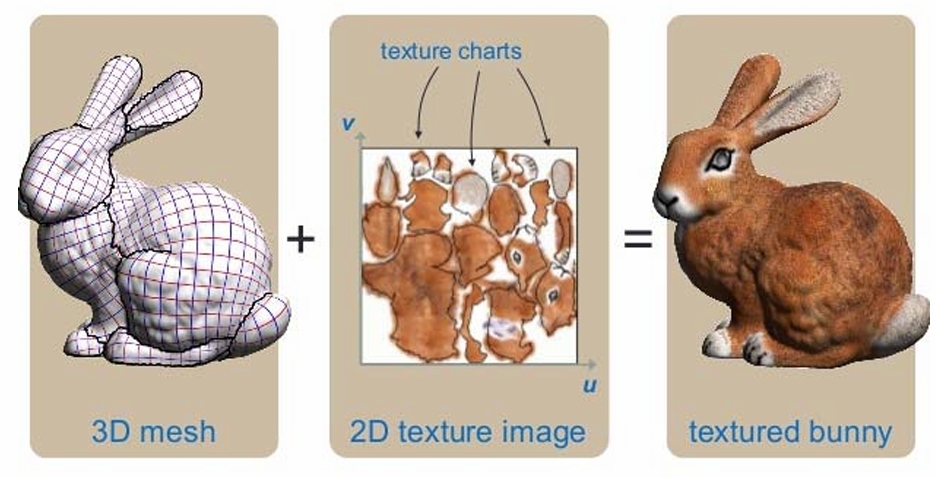
参数化应用：纹理映射：

Constrained (Feature‐Preserving) Global Laplacian Smoothing （约束(保特征)拉普拉斯整体光滑）

有约束的拉普拉斯光滑（固定一些约束点，顶点约束、面约束等）

包括软约束（可以缓一缓）和硬约束（必须满足）

综合一下（其实就是在矩阵下面再加约束方程）：