GAMES102-08-离散微分几何

Lecture 08 Discrete Differential Geometry

三角网格曲面的两种理解：

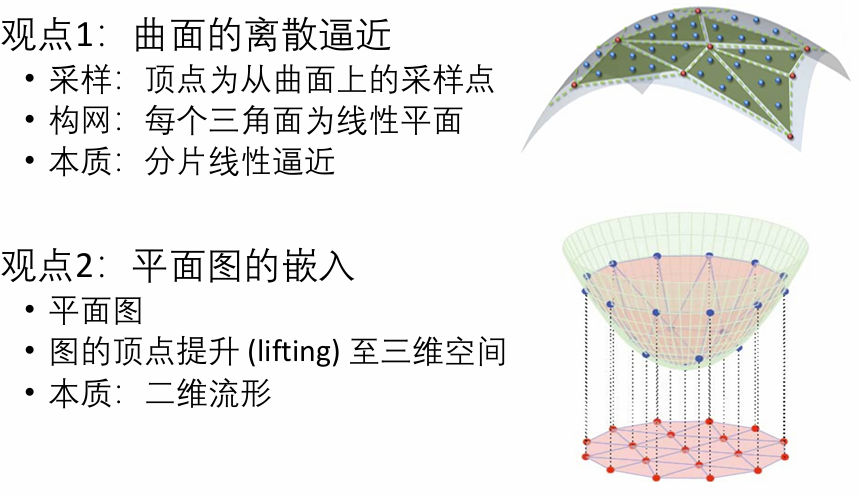
G{V, E, F}：V-顶点集合 E-边集合 F-三角形集合

多边形网格均可转化为三角网格（不考虑流形结构）

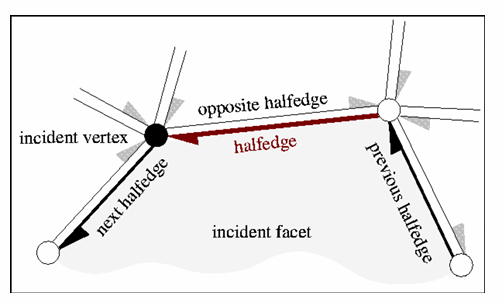
半边数据结构：以“边”为中心的数据结构

• 网格连接关系存储在边上，每条边表达为两条“半边”
• 目的：提高点线面的查询或增删改操作的效率

几何（网格）处理库：

曲线曲面的微分几何

法向：

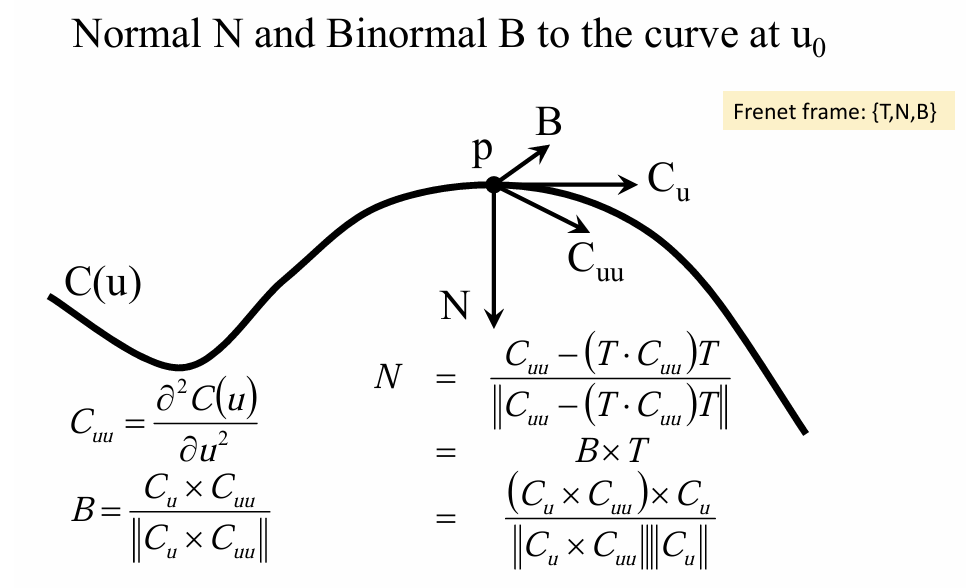
曲率：曲线形状由曲率决定

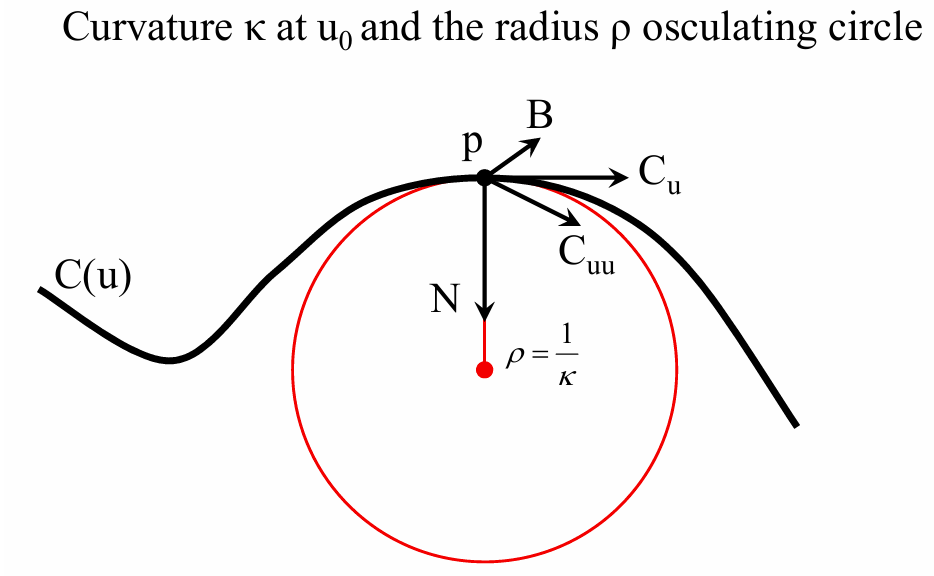
方向曲率：曲率是随着方向变化的

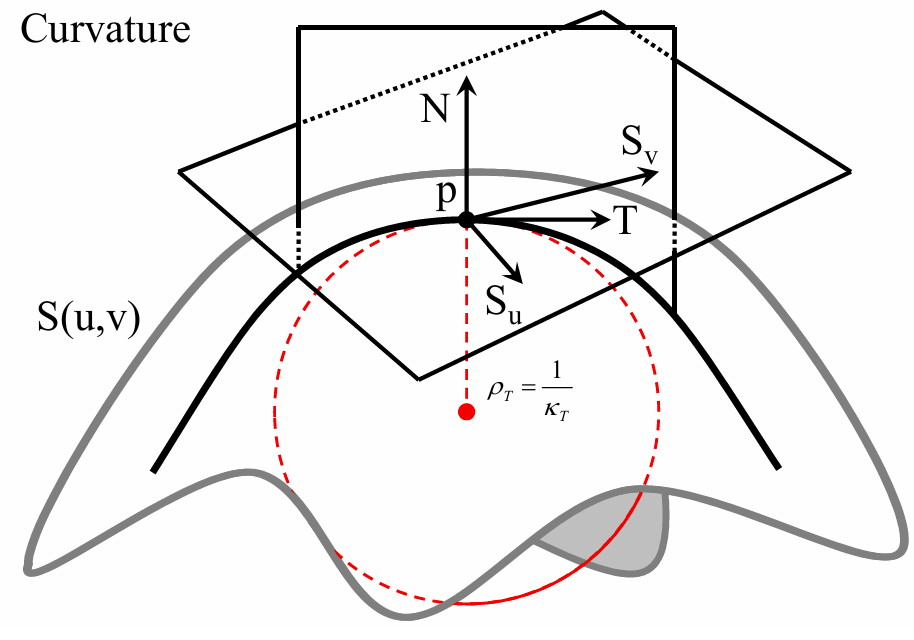
曲面的曲率：

离散微分几何

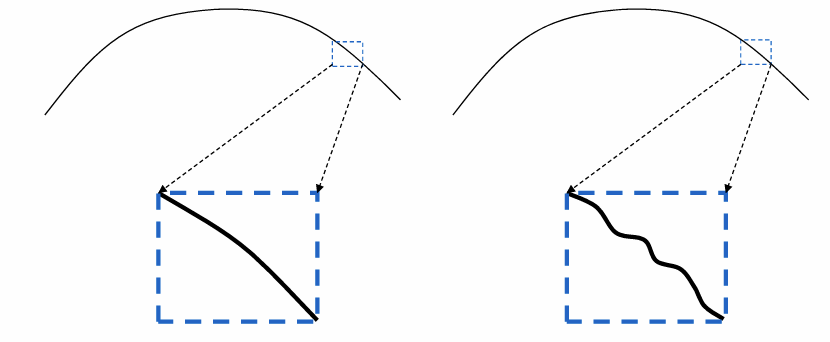
从光滑曲面上采样的离散点只有C⁰连续，但希望通过不可微的离散点得到原来光滑曲面的微分属性

方法：

• 连续逼近
• 离散逼近（这节课主要研究内容）

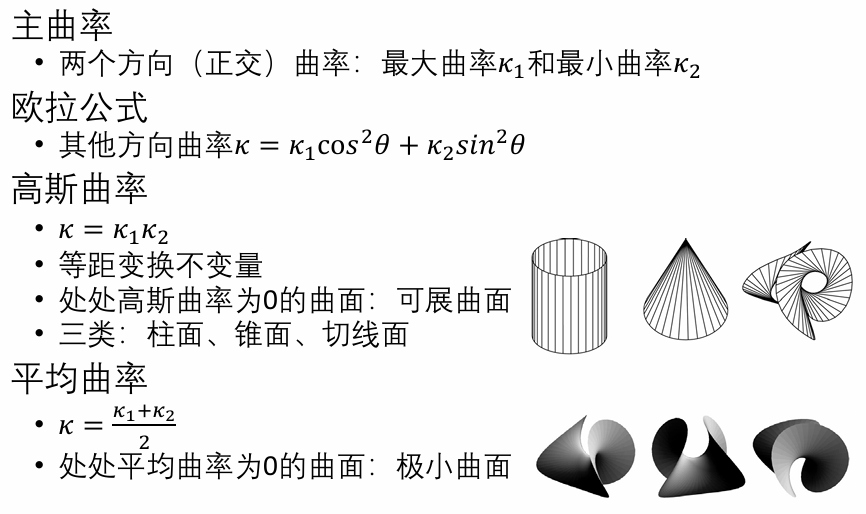
平均曲率（Mean Curvature）：

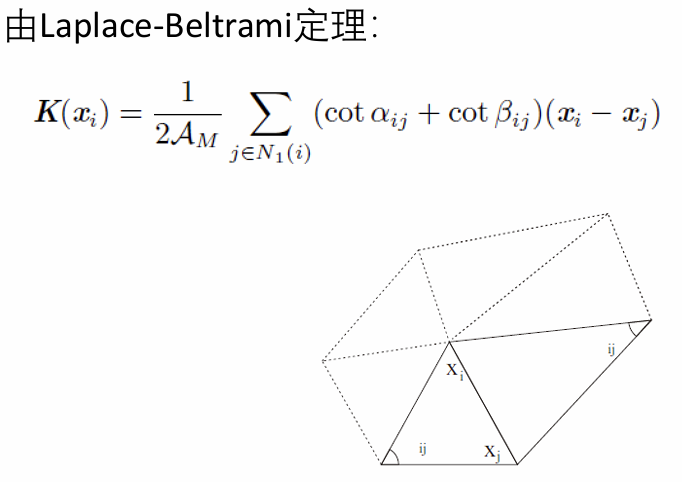
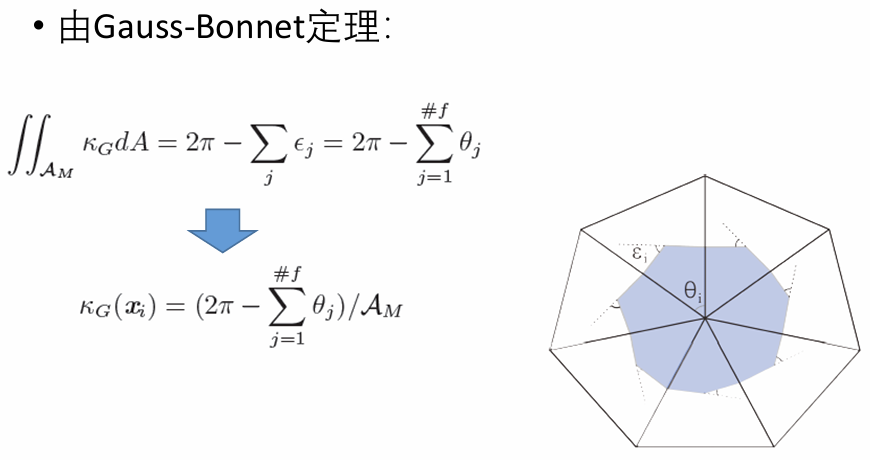
高斯曲率（Gauss Curvature）：

极小曲面：平均曲率处处为0的曲面

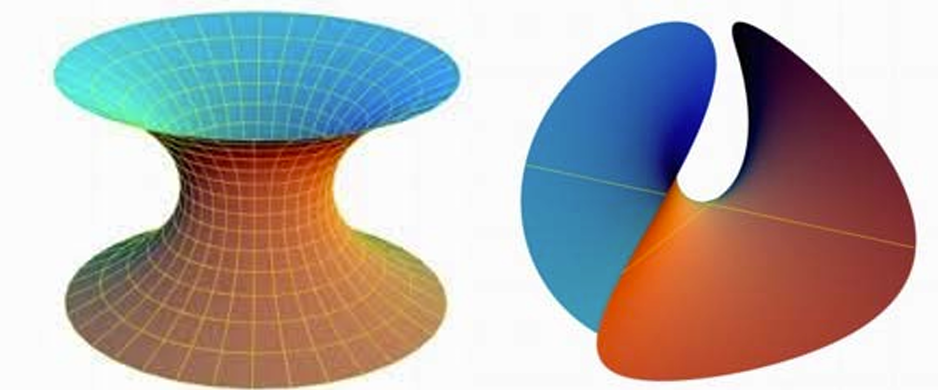
极小曲面及平均曲率流：

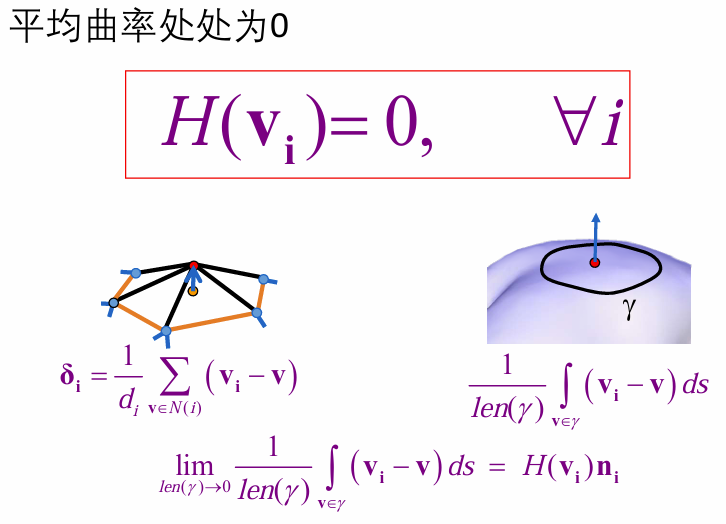
离散平均曲率流：极小曲面求解方法

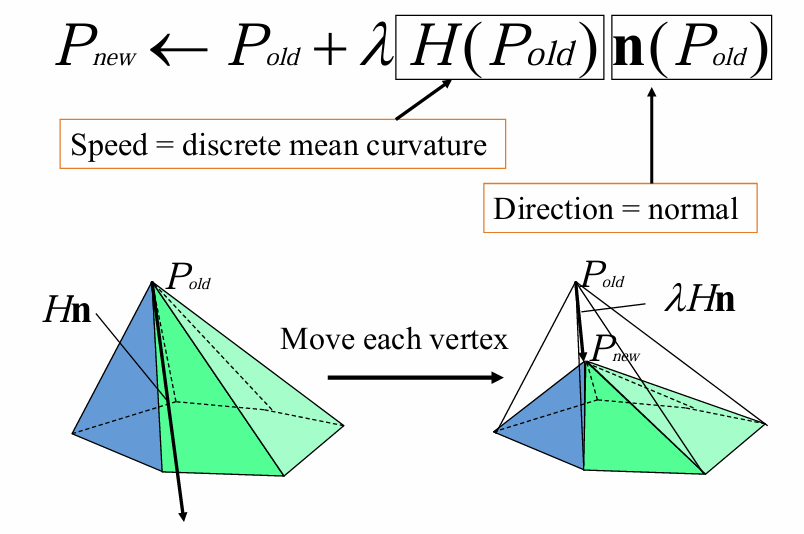
离散极小曲面的局部迭代法

1. 找到边界
2. 固定边界顶点
3. 对每个内部顶点
   1. 找顶点1‐邻域
   2. 更新其坐标
4. 迭代
5. 更新所有顶点法向
6. 回到第三步

需要注意的地方：

• 只能对非封闭曲面（带一条边界）操作
• 更新坐标需要用老的顶点坐标
• 需要尝试试验不同的参数𝜆

后面介绍了科大的自研框架Utopia