Lecture 07 Mesh
光滑(Smooth)曲线:
- 连续曲线:参数连续性(看导数)
- 光滑:高阶连续
- 几何曲线:
- 与参数化无关,更刻画了曲线形状的本征光滑性
- 更适合交互式曲线设计
光顺曲线(Curve fairing):
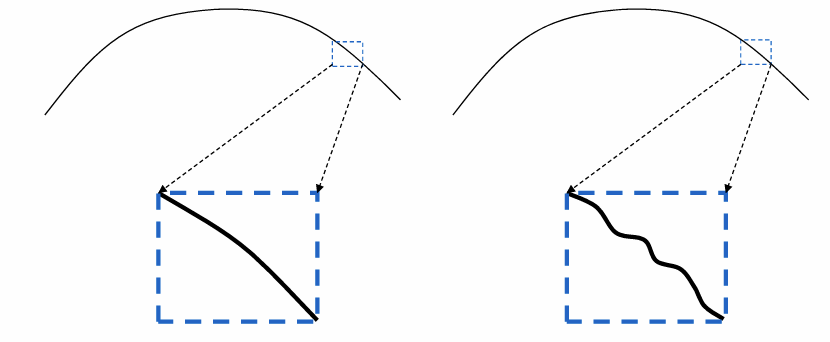
左边光顺右边不光顺(从微观角度上去区分)
光顺没有一个统一的数学定义

曲线的曲率:
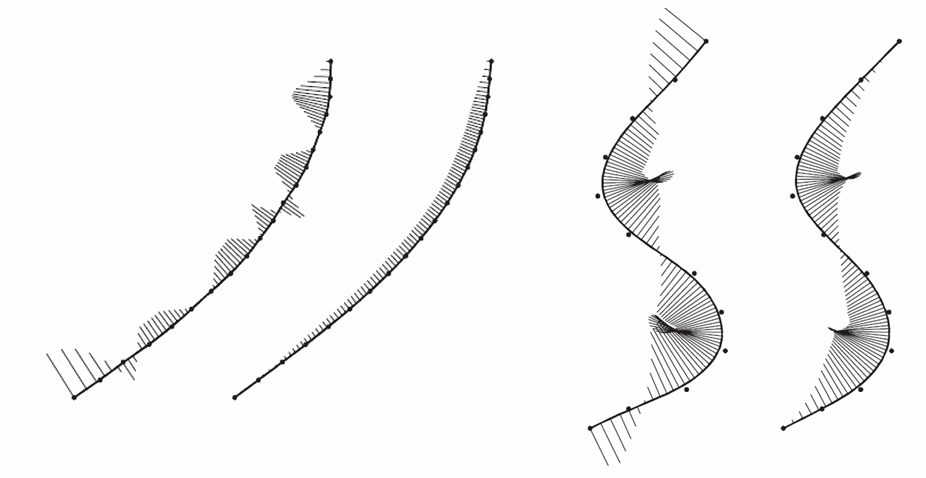
- 从宏观上看两条曲线一致,但从微观上两条曲线的曲率完全不同
对光顺的一些观察:

曲面光顺的新定义:
一条曲线是光顺的,如果
- 它是 C{1+l} ( l > 0 )连续的
- 它的曲线本身拐点较少
- 它的曲率图的拐点较少
- 它的曲率图变化的振幅相对小
曲线的光顺方法:
- 初光顺——定界法
- 基本光顺——卡尺法
- 精光顺——回弹法
曲面的光顺也无严格定义,在工业界叫Class A曲面
实现方法:
- 三向曲线光顺
- 能量法
离散曲线
曲线(形状)的不同表达方法:
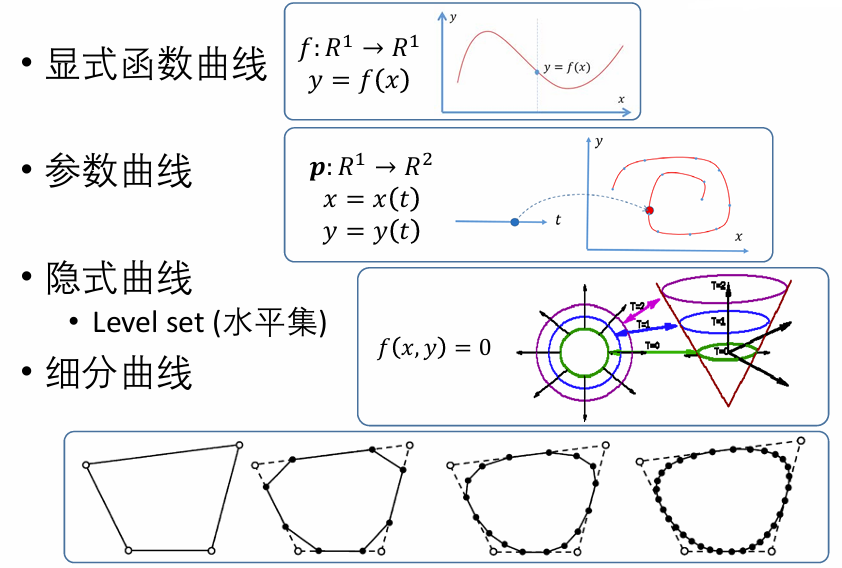
- 几何迭代法(渐进迭代逼近) (progressive‐iterative approximation, PIA)
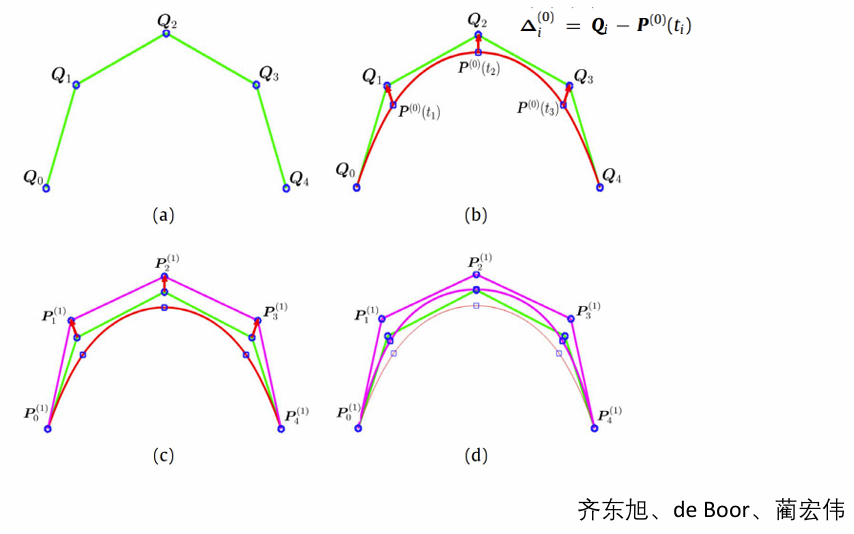
从连续到离散:
- 对象的表达
- 在数学上,连续表达与计算
- 在计算机中,离散表达与计算
- 数值方法:数值微分、数值积分、数值优化
- 数值分析:离散计算对精确计算的近似程度
- Fourier分析/变换:离散Fourier分析/变换
- 卷积(滤波)
- 在计算机科学(计算机图形学)中,采样无处不在
- 计算机只能表达离散的数值
- 例子:int型的数据(量化)
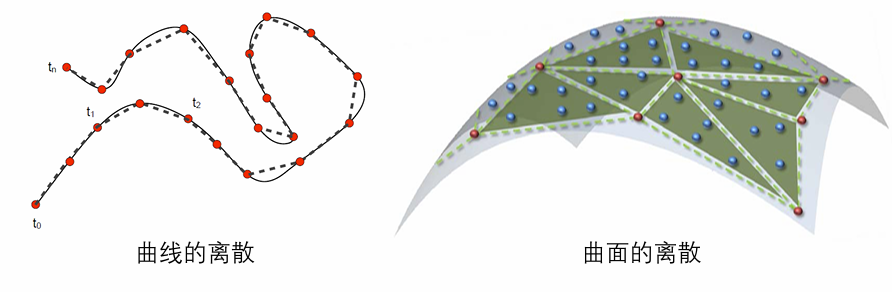
曲线的离散化:将连续性表达转化为多边形表达(分段线性)

为何要离散化?
- 渲染的必要性
- 算法和硬件:线段/圆的光栅
- 计算的必要性
- 直线求交、多项式求根
- 制造的必要性
- 刀具轨迹只能走直线段和圆弧
曲线的离散:采样
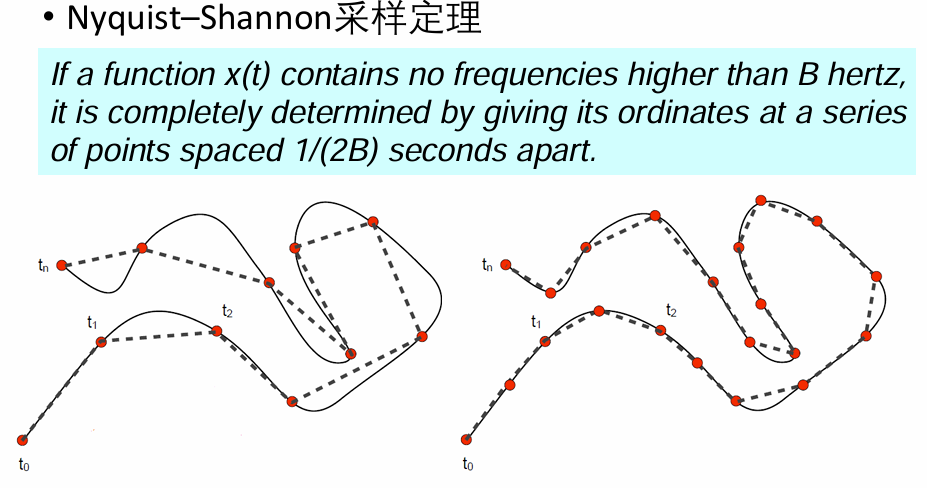
Bezier曲线的离散定理:
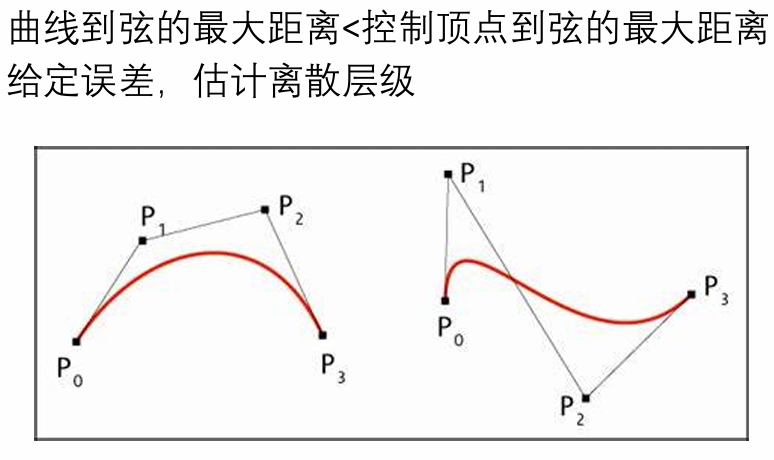
离散曲线的几何量的计算:
- 如果有连续表达,利用连续表达的曲线来计算
- 如无连续表达
- 差分法:利用差分形式来近似微分属性
- 拟合法:利用光滑函数来拟合估计属性
- Tylor展开及估计
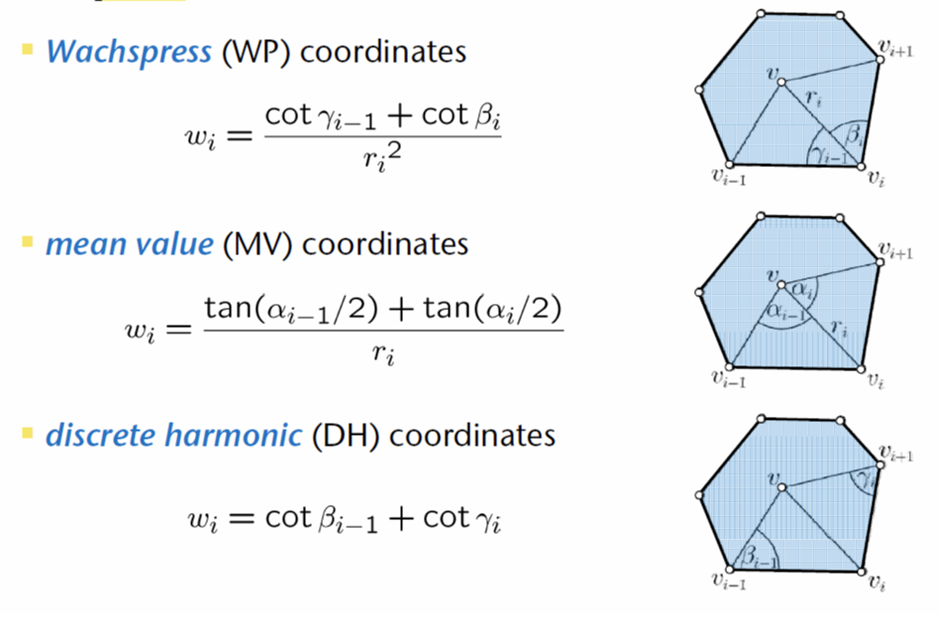
重心坐标:一种用于描述空间中点的位置的方法,特别是在多边形或多面体内部,即描述内部点与边界点(控制顶点)之间的关联关系。

重心坐标的应用:
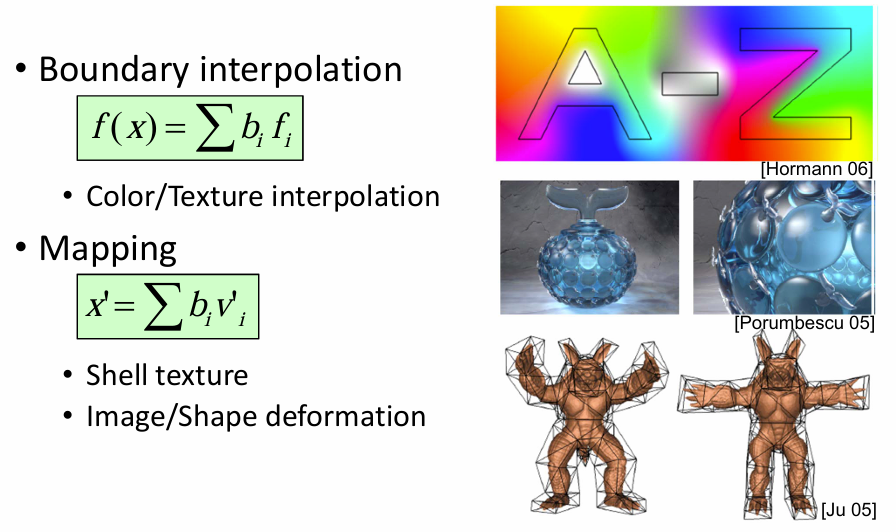
各种重心坐标的计算方法:
三角网格
绘制:离散表达
- 曲线的绘制:
- GDI/OpenGL 绘制基本单元:点、线段
- 曲线须离散成多边形
- 曲面的绘制:
- OpenGL 绘制基本单元:点、线、三角形
- 曲面须离散成三角形网格
流形(Manifold):流形是一个局部类似于欧几里得空间的拓扑空间。具体来说,一个流形满足以下条件:
- 拓扑空间:流形是一个拓扑空间,这意味着它具有开集、闭集等拓扑结构。
- 局部欧几里得性:在流形的每个点附近,都存在一个开集,这个开集与欧几里得空间中的开集同胚(即存在连续的双射,其逆也是连续的)。
- 维度:流形具有固定的维度,即在每个点的邻域内,它都与相同维度的欧几里得空间同胚。
流形的例子包括:
- 平面、球面、环面等几何体。
- 地球表面,尽管地球是一个三维空间中的球体,但在局部范围内,地球表面可以被看作是一个二维流形。
- 某些复杂的几何形状,如莫比乌斯带,也是二维流形。
非流形(Non-manifold):非流形是指不满足流形定义的空间。它们可能在某些点或区域不具有局部欧几里得性质,或者在不同点的邻域具有不同的维度。非流形的例子包括:
- 具有边界的空间:例如,一个开放的立方体(不包括其边界)是一个三维流形,但如果包括边界,它就不再是流形,因为边界点不满足局部欧几里得性质。
- 具有奇点的空间:例如,一个圆锥在顶点处不满足流形的定义,因为顶点处的邻域不与任何欧几里得空间同胚。
- 不规则形状:某些不规则或分形形状可能在某些区域不满足流形的条件。
区别:
- 局部性质:流形在每个点的邻域内都具有与欧几里得空间相同的局部结构,而非流形可能在某些点或区域不具有这种结构。
- 维度一致性:流形在整个空间中具有一致的维度,而非流形可能在不同区域具有不同的维度。
- 拓扑结构:流形具有更严格的拓扑结构要求,而非流形可能在拓扑上更加复杂或不规则。
往后提的处理都是针对流形的,如果存在非流形就把它去掉
定义一个网格:
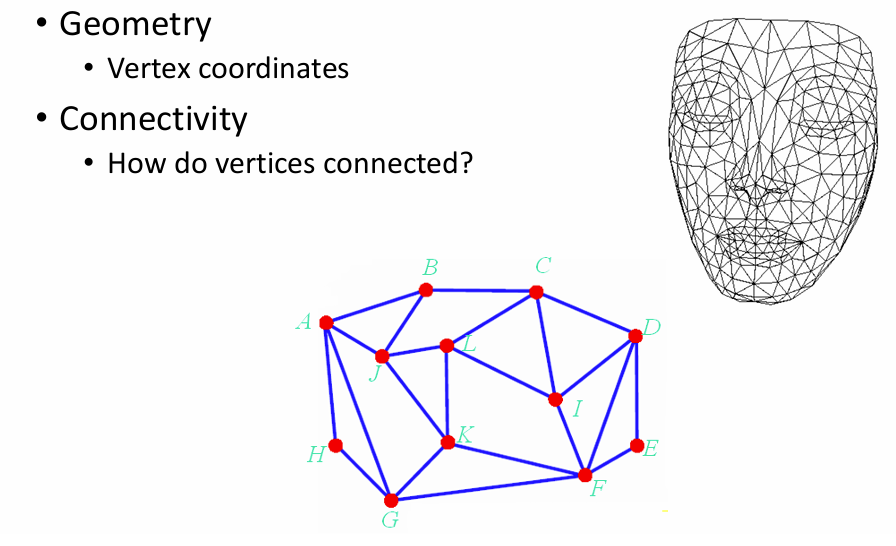
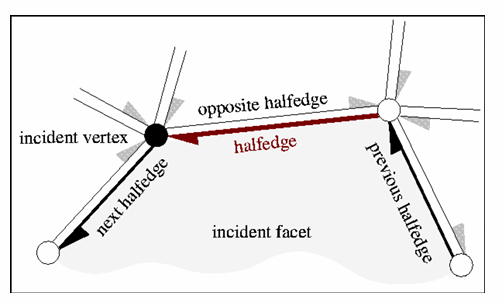
存储网格有很多方式,可以直接用成熟的框架
用的最多的结构是半边(half-edge)数据结构