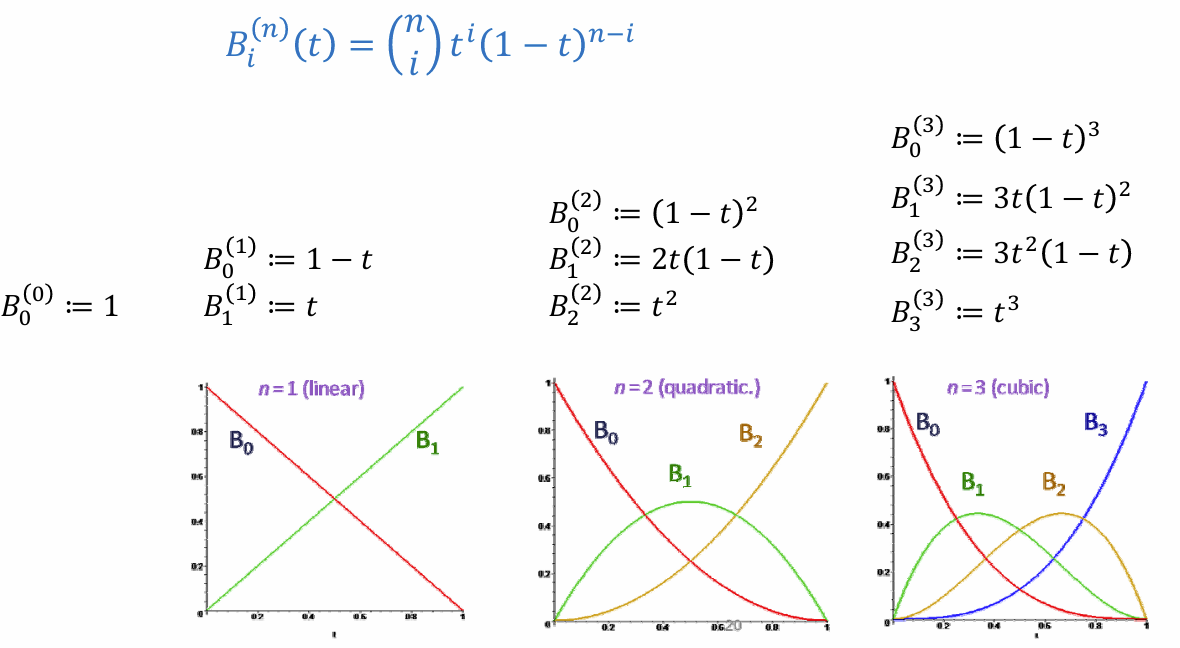
Lecture 06 Many-Splines
有理曲线
Bézier曲线无法表示精确的圆弧
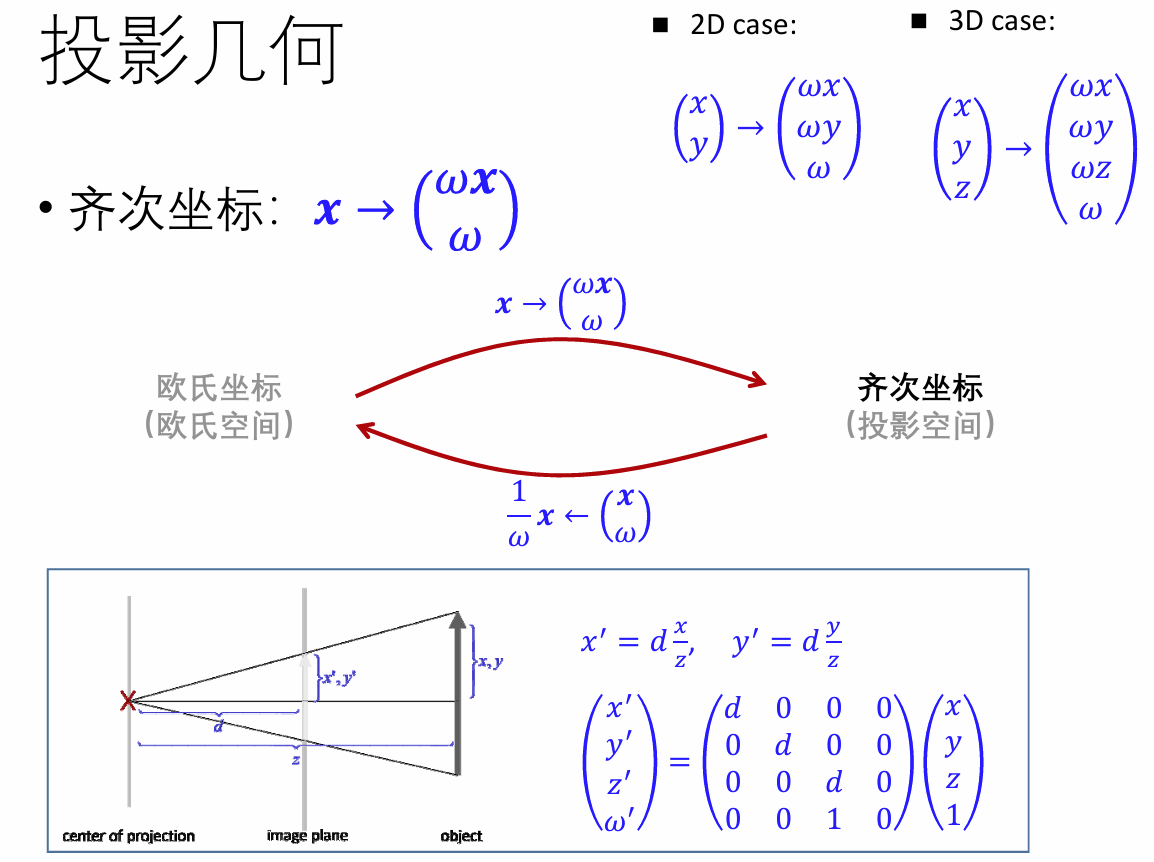
有理Bezier曲线:在高维空间定义曲线再投影回来
- 在 Rn 空间中定义了一个度数为 d 的有理Bezier曲线
- 首先在 (n+1) 维空间中形成一个度数为 d 的Bezier曲线
- 将最后一个坐标解释为齐次分量
- 通过投影得到欧几里得坐标
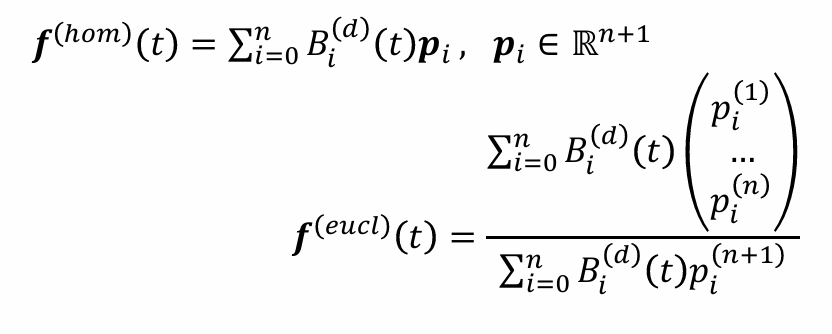

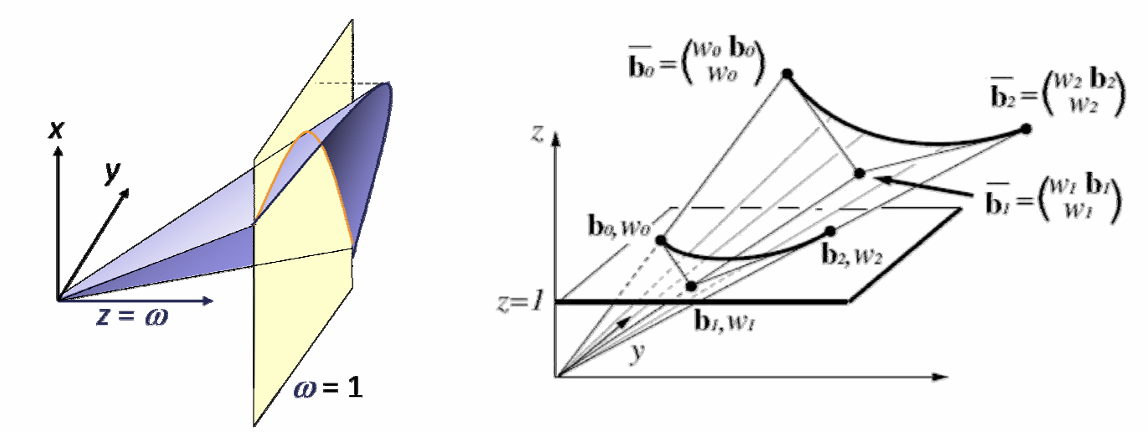
有理Bezier曲线的几何解释:高维的Bezier曲线的中心投影
权系数对曲线形状的影响:控制顶点的权系数越大,曲线就越靠近该点
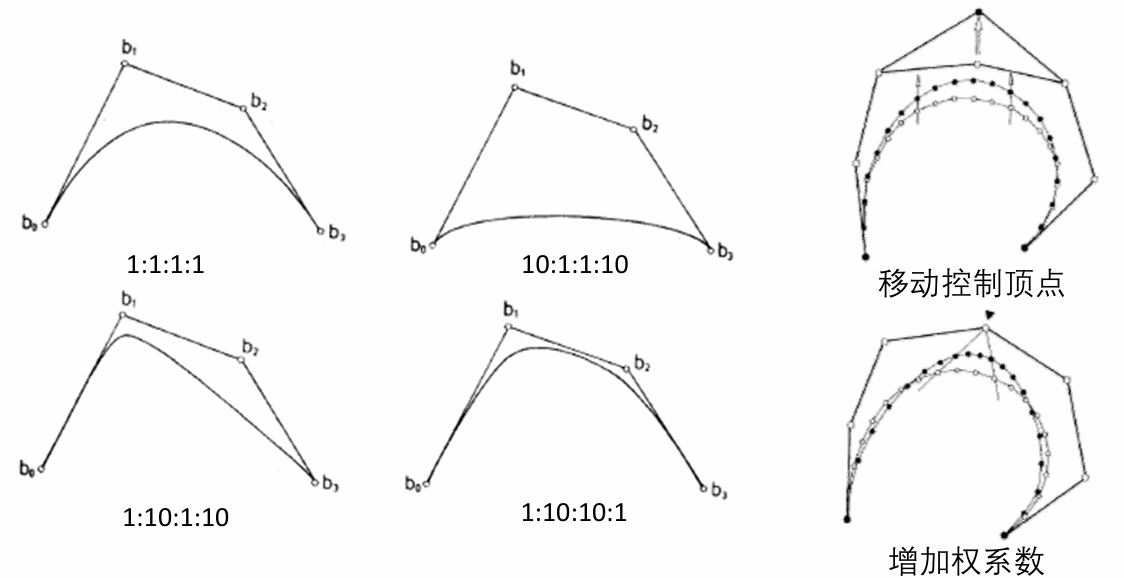
有理Bezier曲线的性质:具有Bezier曲线的大部分性质
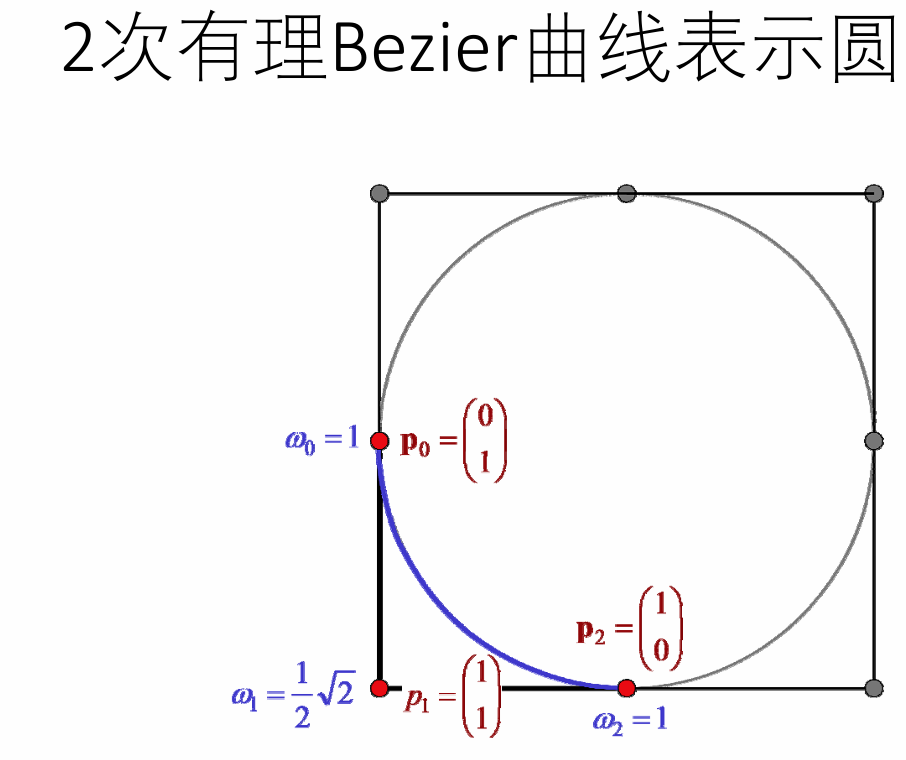
NURBS曲线
NURBS: Non‐Uniform Rational B Spline (非均匀有理B样条)
NURBS曲线的表达式:
其中 Ni,pa(t) 是B样条基函数,wi 是权重,Pi 是控制点
- 与B样条的结点序列等保持不变
- De Boor算法类似于有理de Casteljau算法
- 在计算过程中可以:
- 选择1:分别对分子和分母应用De Boor算法
- 选择2:在每个中间结果中归一化权重
- 第二个选项在数值上更稳定
- 影响NURBS曲线建模的因素:
- 控制顶点:用户交互的手段
- 节点向量:决定了B样条基函数
- 权系数:也影响曲线的形状,生成圆锥曲线等
NURBS曲线的性质大部分与Bezier/B样条曲线类同:具有良好的几何直观性
NURBS曲线的例子:
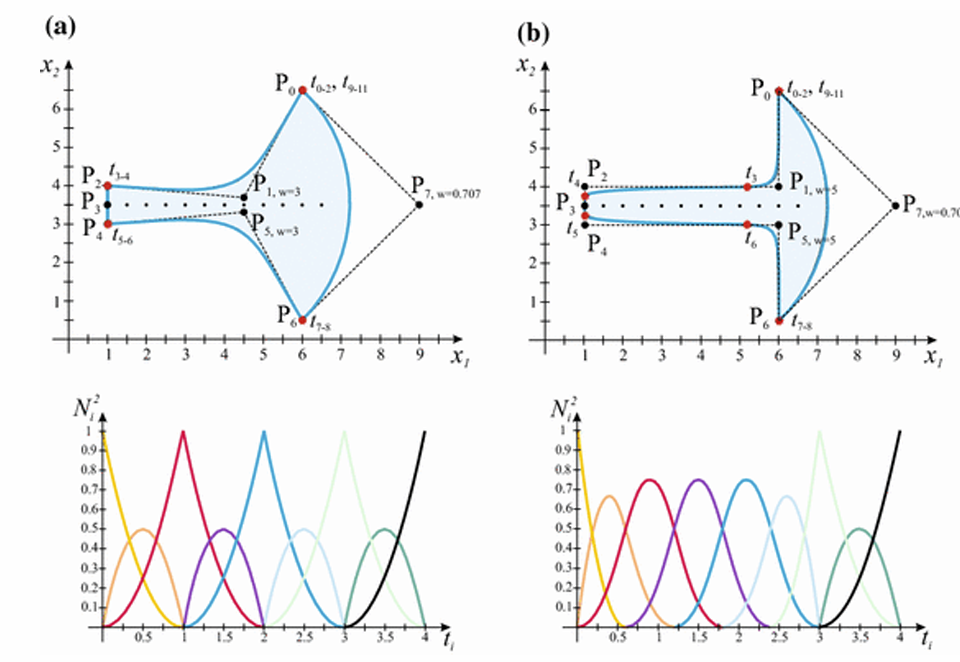
NURBS曲线/曲面表达是当前的工业标准
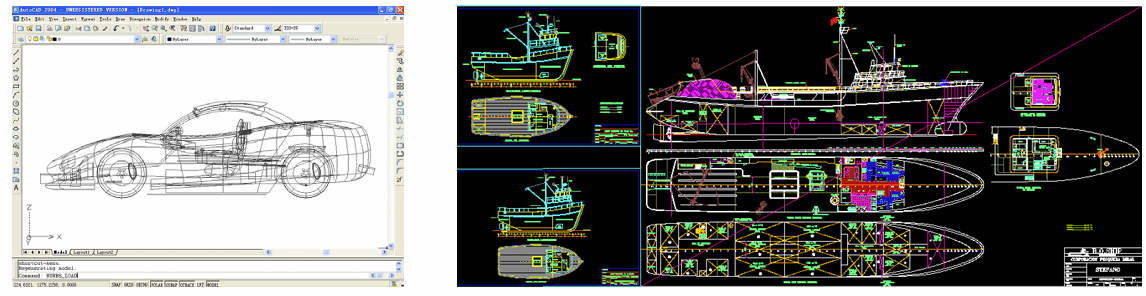
细分曲线
de Casteljau作图算法从几何直观性来说类似雕塑雕刻过程:逐步割角、磨光
启发:是否可以通过不断“割角”构造曲线?
- 给定一个简单多边形
- 通过一定规则,割角磨光,产生更多边的多边形
- 不断迭代操作割角磨光,产生(极限)光滑曲线
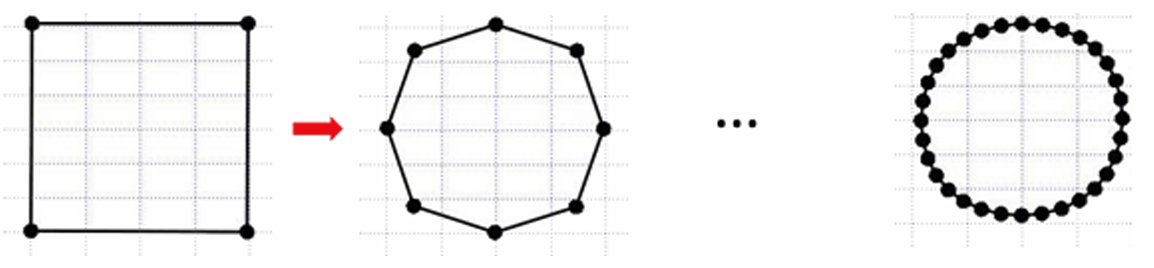
细分方法的思想:
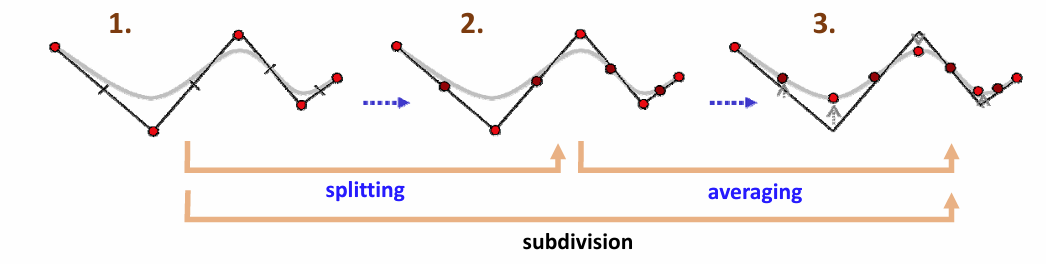
两个步骤:
- 拓扑规则:加入新点,组成新多边形(splitting)
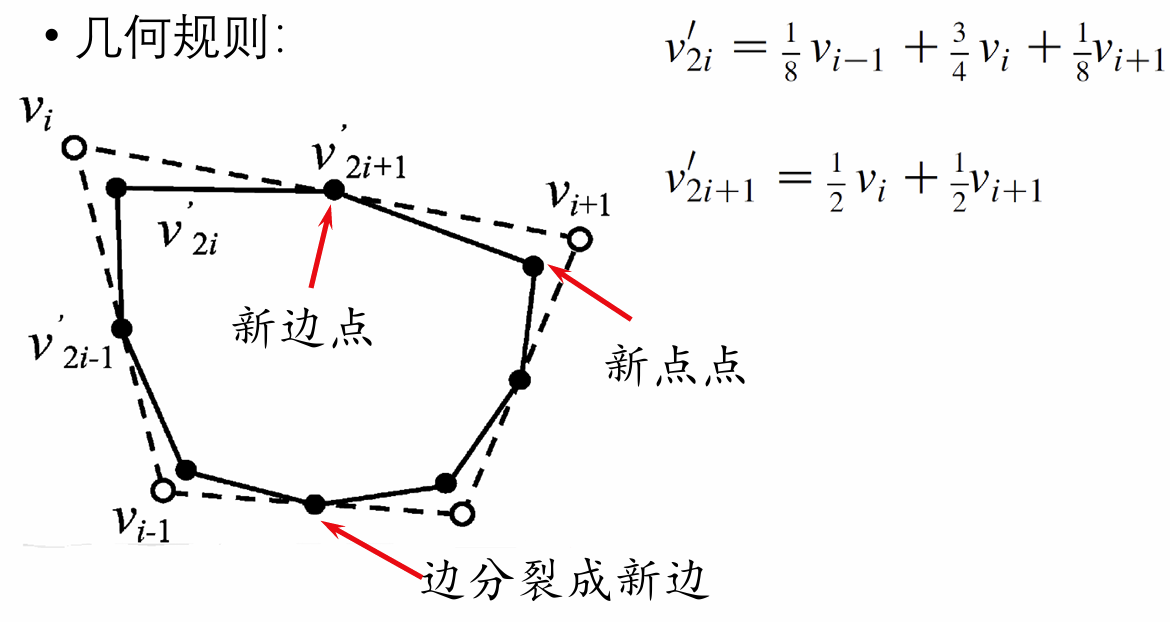
- 几何规则:移动顶点,局部加权平均(averaging)
- 对所有顶点都移动:逼近型
- 只对新顶点移动:插值型
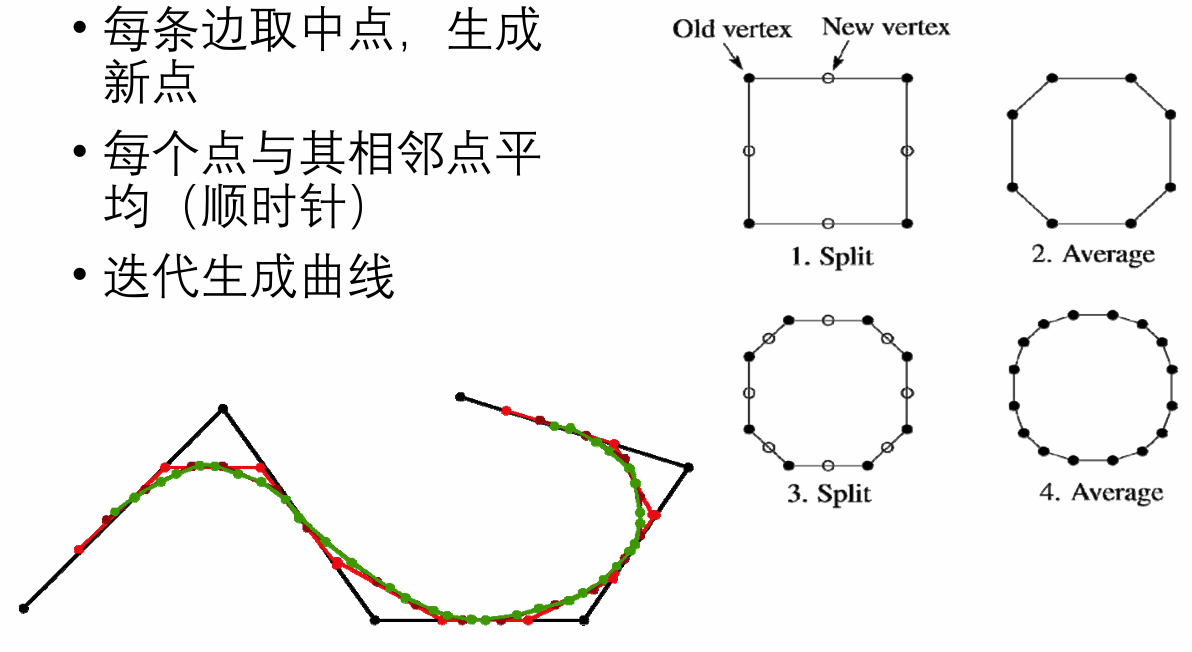
Chaikin细分方法(1974年提出):
- 拓扑规则:
- 点分裂成边(割角),老点被抛弃(逼近型)
- 新点老点重新编号
- 几何规则:新顶点是老顶点的线性组合
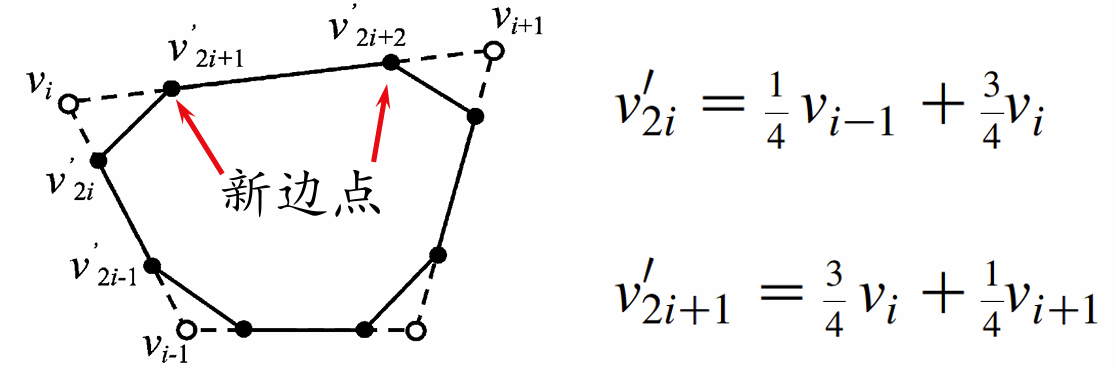
可以证明:
- 极限曲线为二次均匀B样条曲线
- 节点处C1,其余点处C∞
均匀三次B样条曲线细分方法:
- 拓扑规则:边分裂成两条新边
- 几何规则:点重新算位置
细分曲线的性质的证明思路:
- 将细分过程表达成矩阵形式:新顶点是老顶点的线性组合
- 讨论细分矩阵的谱性质(特征根)
- 极限情况:极限曲线上的点可由细分矩阵的幂次的极限求得
- 收敛的必要条件:细分矩阵的最大特征根为1,否则会爆炸(>1) 或收缩(<1)
插值型细分方法:可以看成是“补角法”
- 保留原有顶点
- 对每条边,增加一个新顶点
- 不断迭代,生成一条曲线
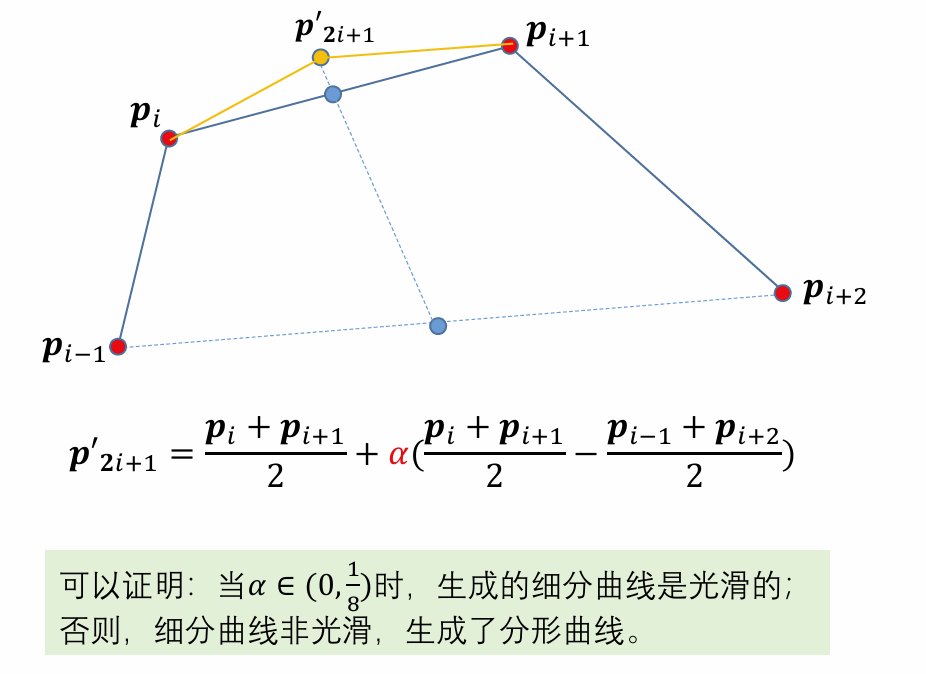
4点插值型细分规则(1987年提出):
4点细分曲线的例子:
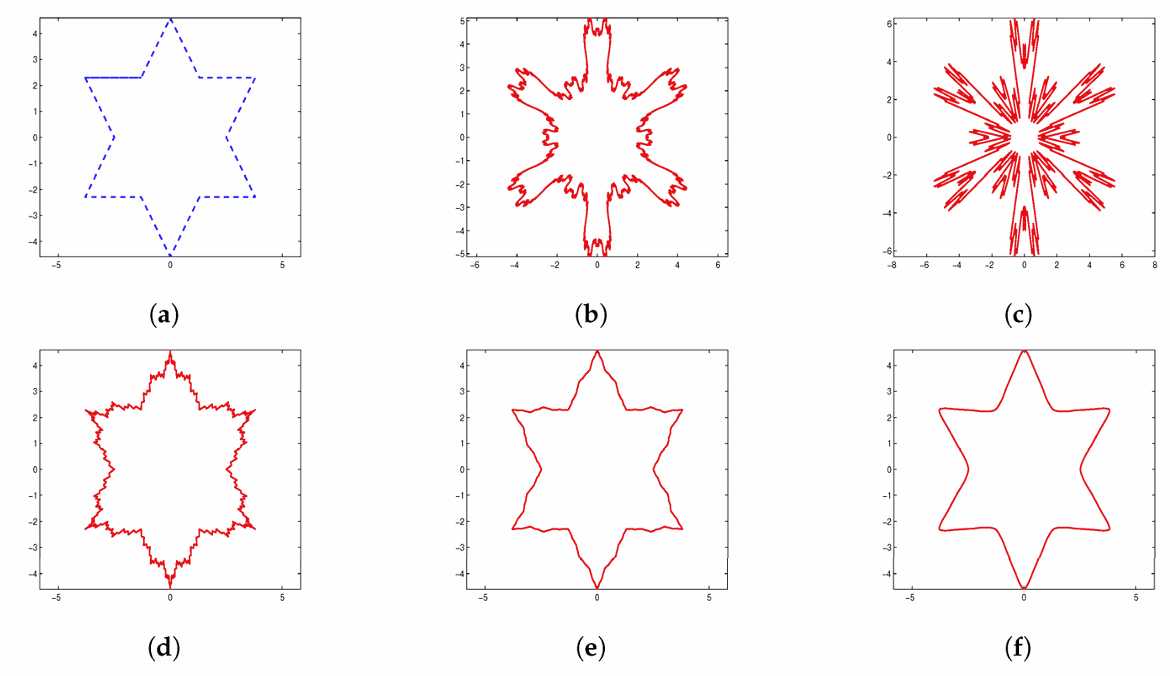
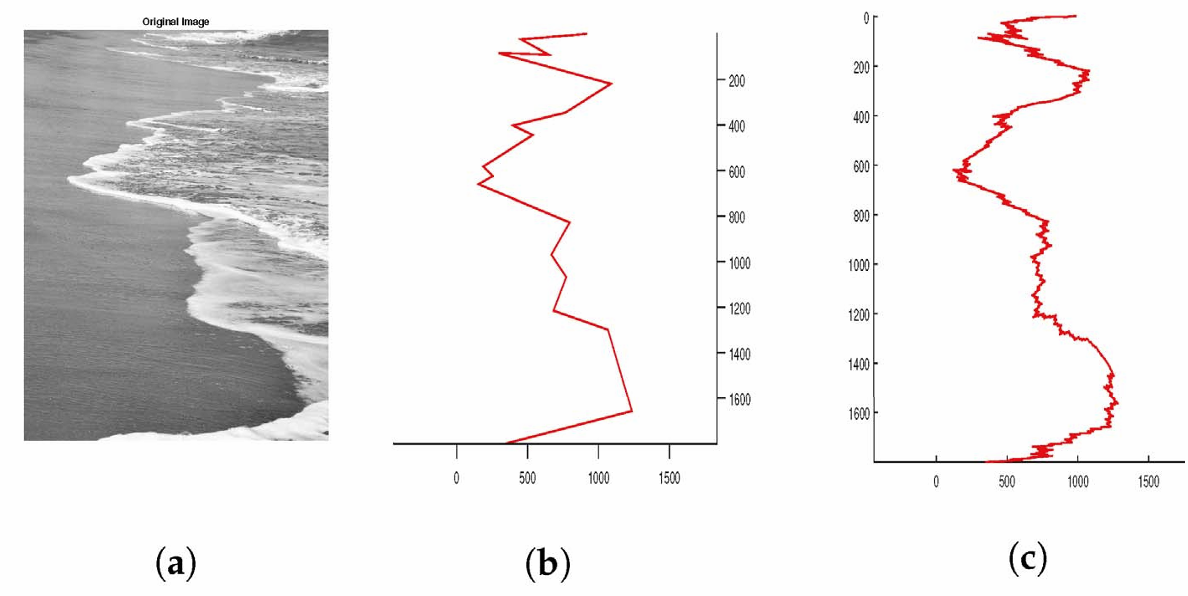
分形曲线(分数维):分形几何
英国的海岸线到底有多长?不同尺度测量结果差异极大
IFS:自迭代函数系统,一个函数不断迭代就能产生分型效果
一般:2n点插值细分方法

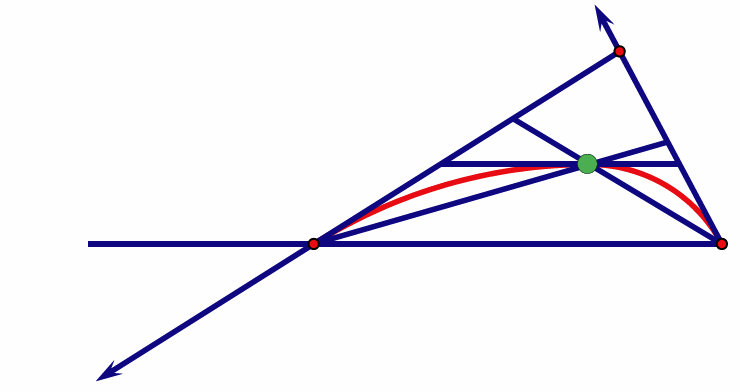
非线性细分方法:基于双圆弧插值的曲线细分方法
- 给定一条边,新点为插值其两端点及两端切向的双圆弧的一个连接点,也是其两端点两端切向的所确定三角形的内心
- 每个细分步骤后调整切向
隐式曲线
隐式函数:自变量x和应变量y的关系非显式关系,是一个 隐式的关系(代数方程)
f(x, y) = 0
所有满足该代数方程的点的轨迹是条曲线
隐式曲线:
将隐函数升高一维,可以看成是x和y的二元函数
z = f(x, y), x, y ∈ [a, b] × [c, d]
则该隐函数曲线是上述二元函数的0等值线,即平面z=0与z=f(x,y)的交线:
f(x, y) = 0
- 在曲线上:f(x,y) = 0
- 在曲线的左侧(内部):f(x,y) < 0
- 在曲线的右侧(外部):f(x,y) > 0
可以用于定义符号距离场(Signed Distanse Field, SDF)
隐函数的性质:
- 考虑曲面上的一个点 x,满足 f(x)=0
- 梯度非零假设:假设
- ∇f(x) = 0
- 单位法向量:隐式曲面的单位法向量为:
- 对于有符号函数,法向量指向外部
- 对于有符号距离函数,上述公式简化为 n(x) = ∇f(x)
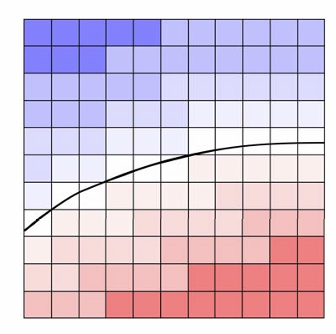
隐式曲线的绘制:
- Marching Cubes算法(1987年提出)
- 隐式曲线绘制的最常用方法
- 思想(2D: Marching Squares)
- 在一些离散格子点上求值
- 然后利用局部连续性插值出值为0的点
- 按一定的顺序连接这些点形成离散曲线

隐式曲线拟合:
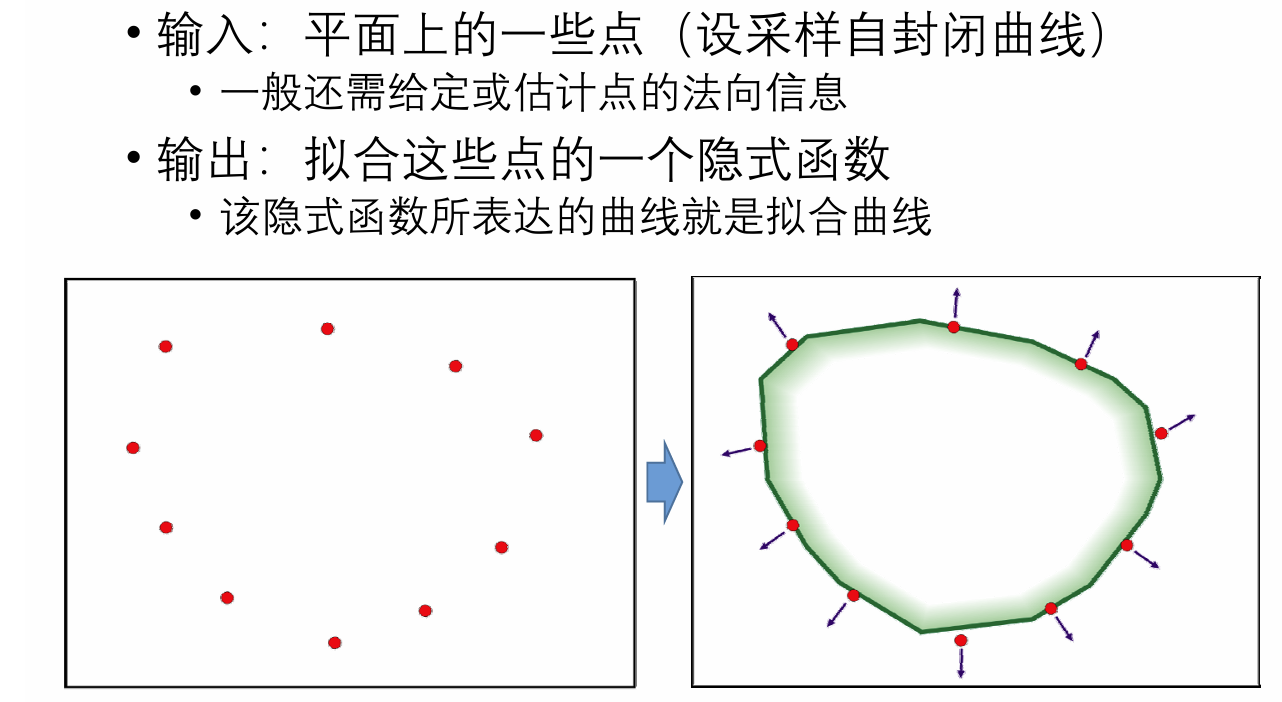
求解步骤:
- 估计法向:利用邻近点来估计切平面
- 拟合一个二元函数:在型值点上值为0,外部(法向方向的点)为正,内部为负
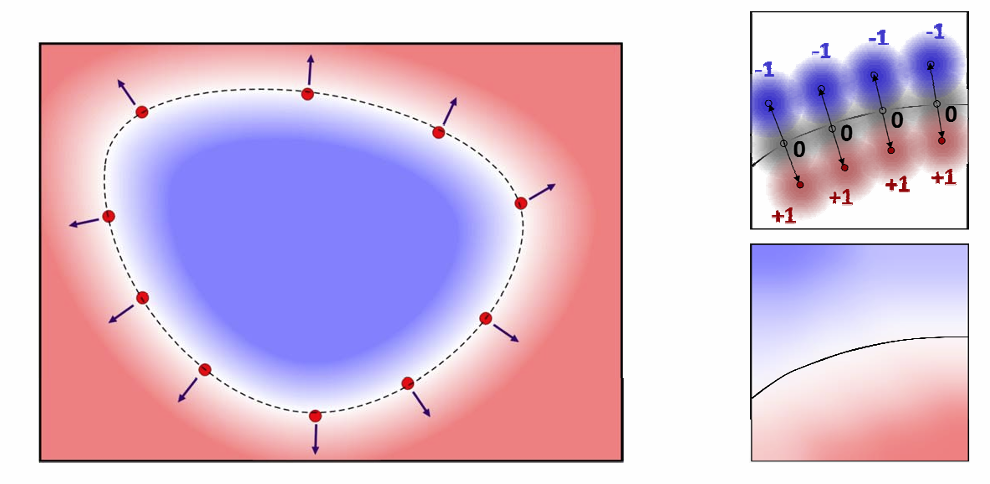
隐函数构造方法:
- Blobby molecules
- Metaball
- RBF based method
- Multi‐level partition of unity implicits (MPU)
- Poisson reconstruction method
- Screened Poisson method
- …
NURBS曲面
回顾:曲线曲面的不同形式
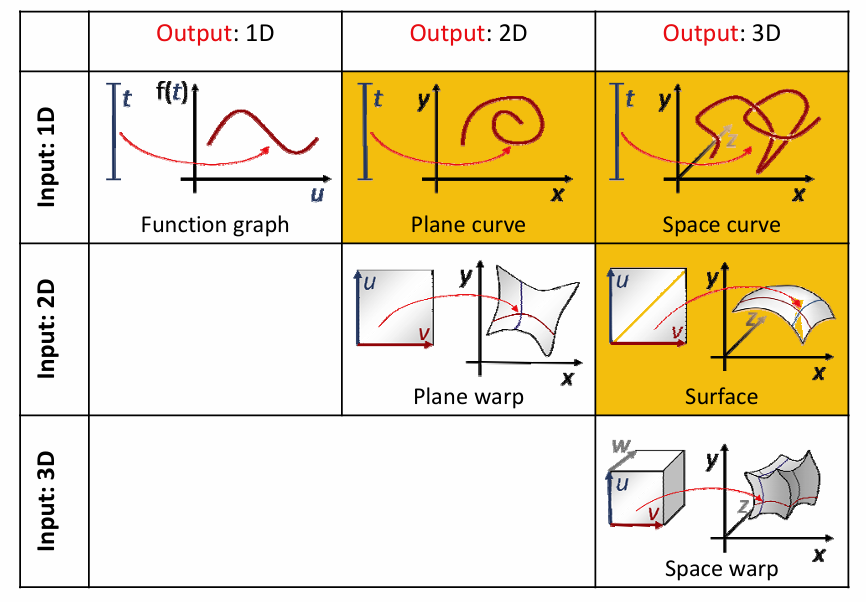
参数曲面:
双参数(u, v)
参数曲面
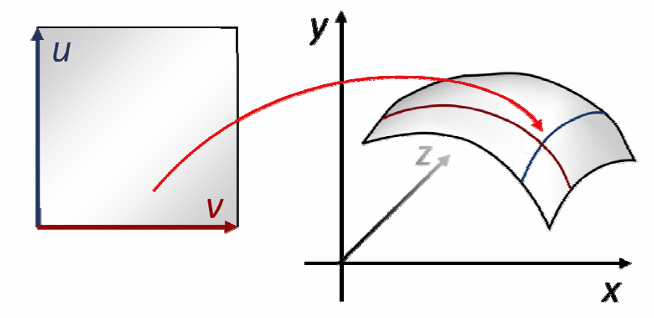
基本方法:张量积
张量积曲面:就是曲线的组合,两个方向两次的组合
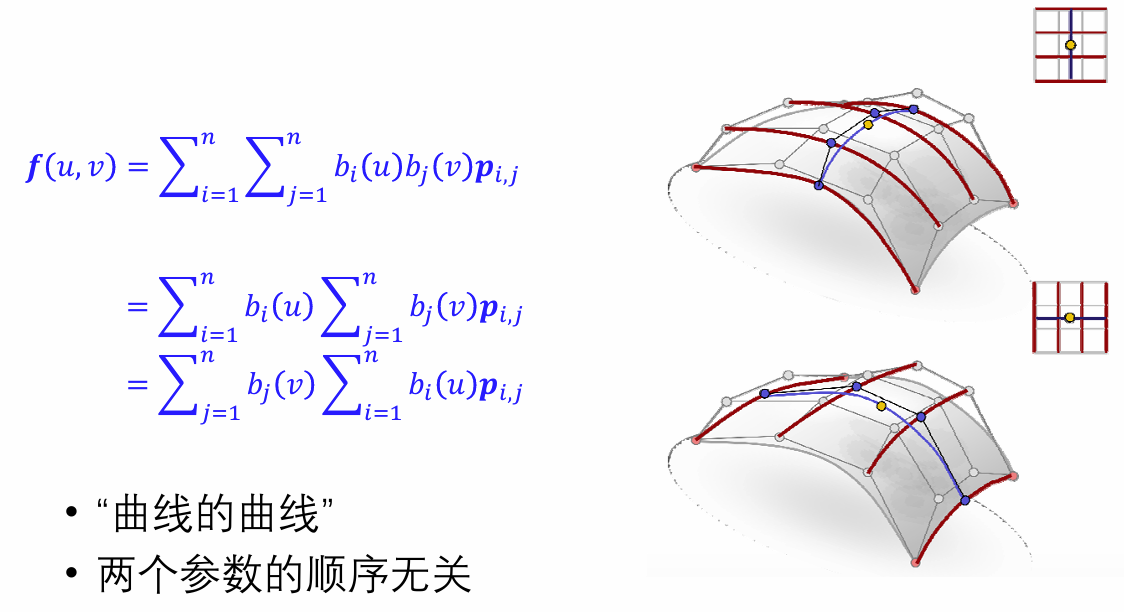
张量积曲面的性质:
- 类似于曲线情形,性质取决于基函数的性质
- 先沿一个方向做,然后再沿另一个方向做(方向顺序无关)
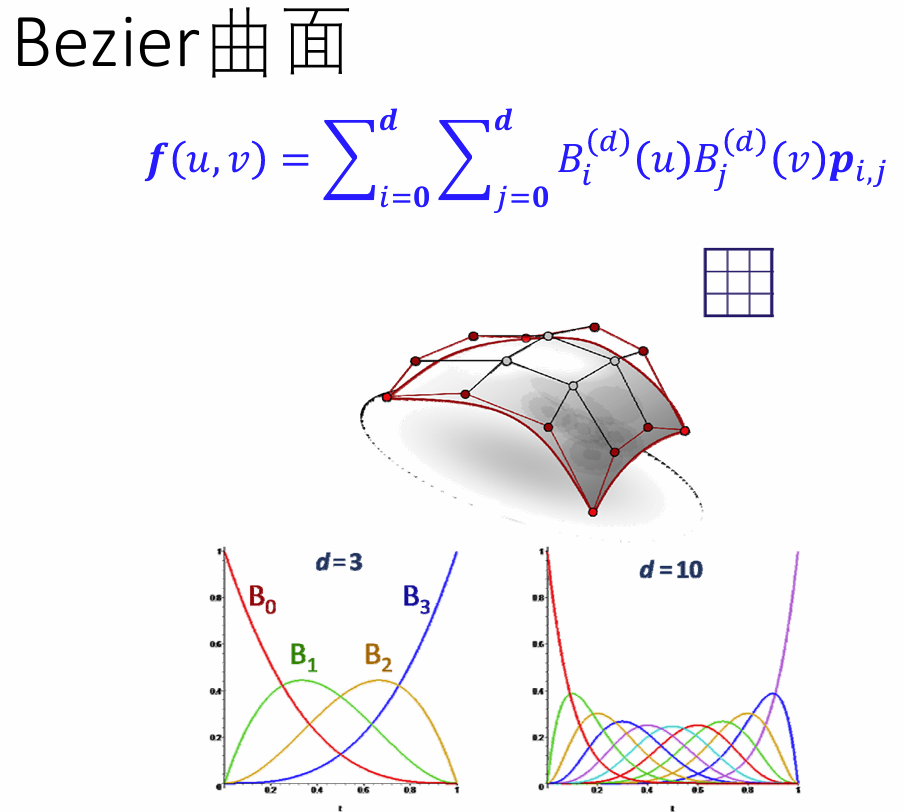
- Bezier曲面片具有类似的良好性质
- 边界插值
- 凸包
- 变差缩减
- 几何作图法
- …
de Casteljau作图法:
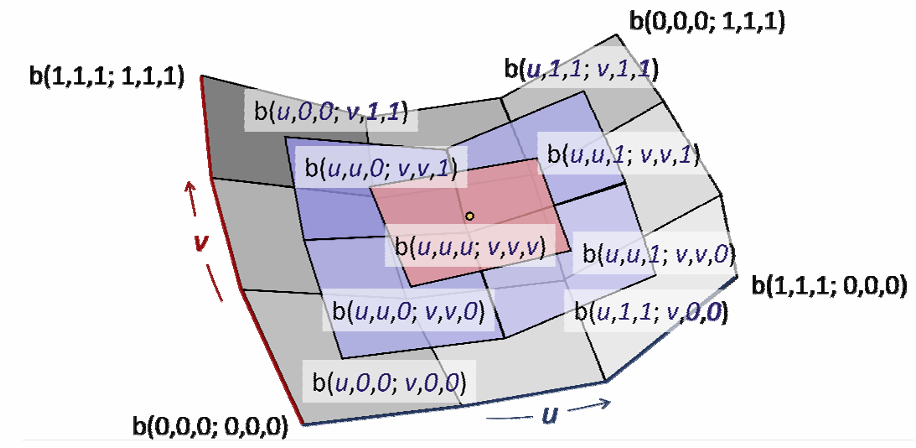
其他曲面的定义完全同:B样条曲面 / 有理曲面 / NURBS曲面
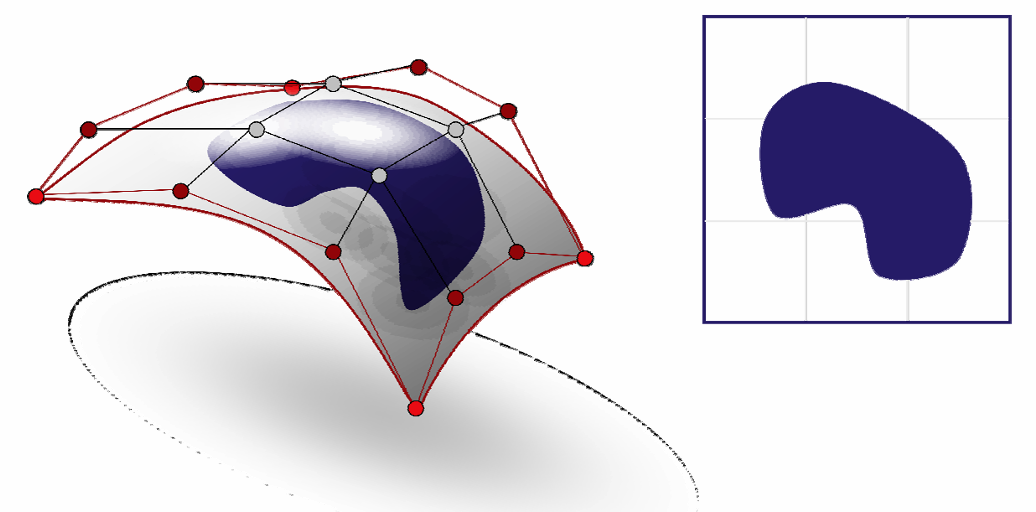
Trimmed NURBS曲面:表达带“洞”或非矩形边界的曲面
- 曲面上的曲线:使用参数域上的NURBS曲线来定义,然后复合得到曲面上的曲线
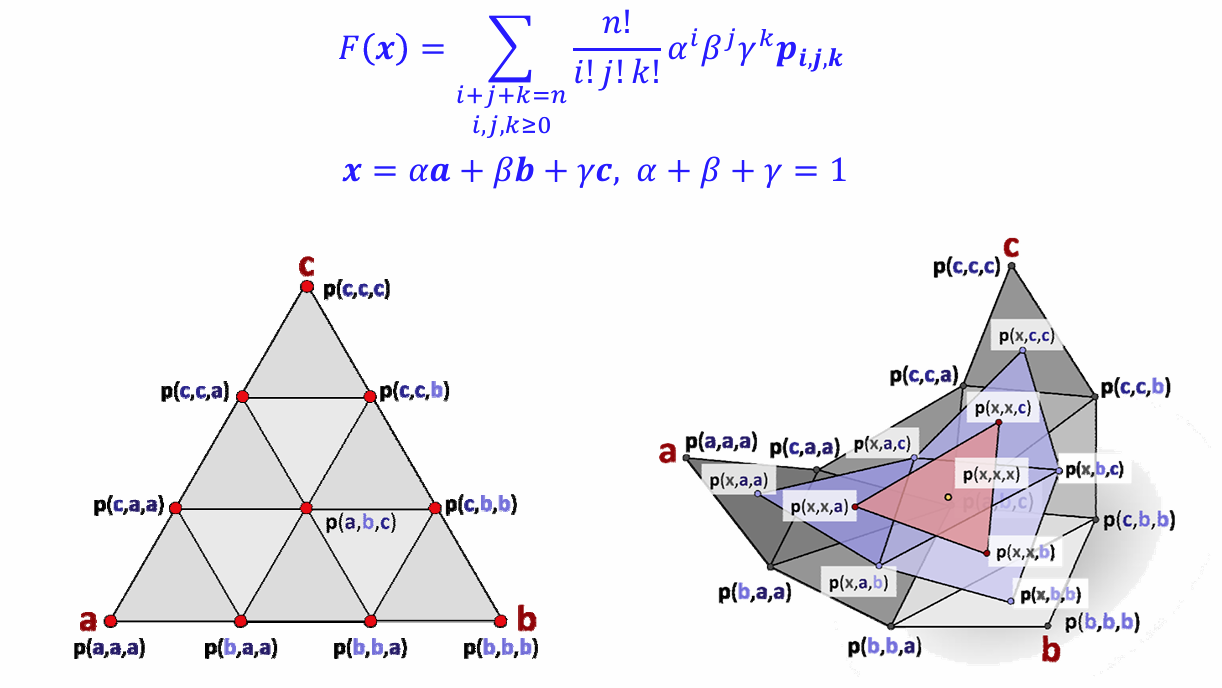
三角域的Bernstein‐Bezier曲面片:
- 矩形域有时不方便
- 使用三角域来定义曲面片
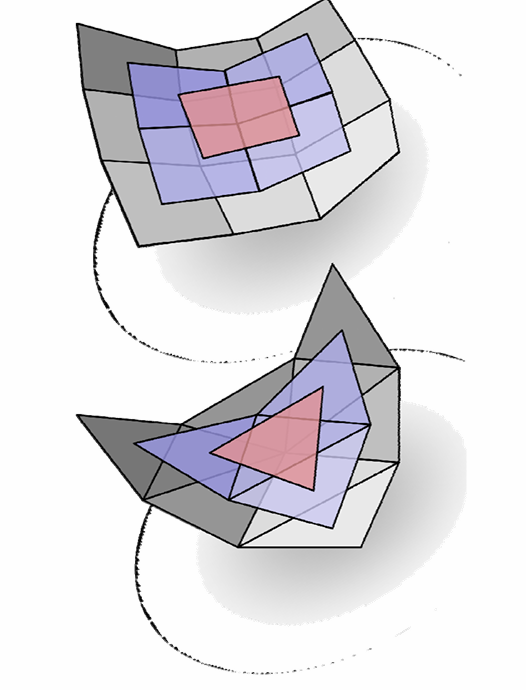
三角Bezier曲面片:
张量积曲面会遇到的特殊问题:角点的光滑性