Lecture 05 B-Spline
建模的两种形式:

曲线拟合从代数观点来看是从一组基函数所张成的函数空间中,找一个“好”的函数来拟合给定的采样点。从几何观点看:

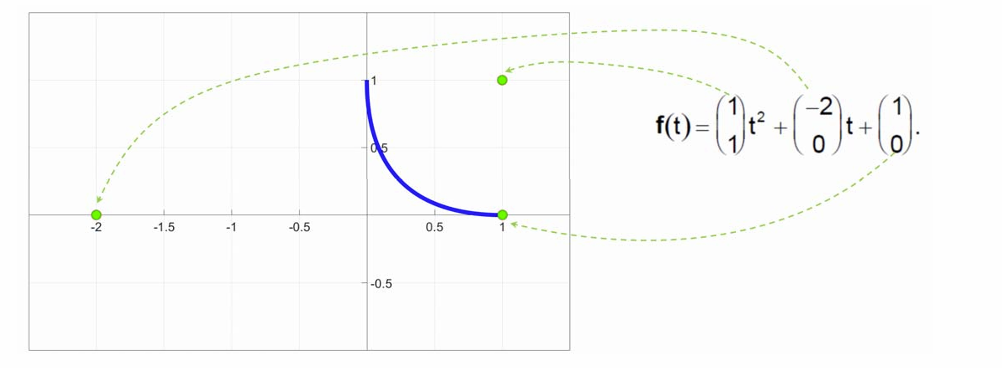
系数顶点与曲线本身无直观的联系,无几何意义 → 不利于用户在设计建模中交互修改曲线

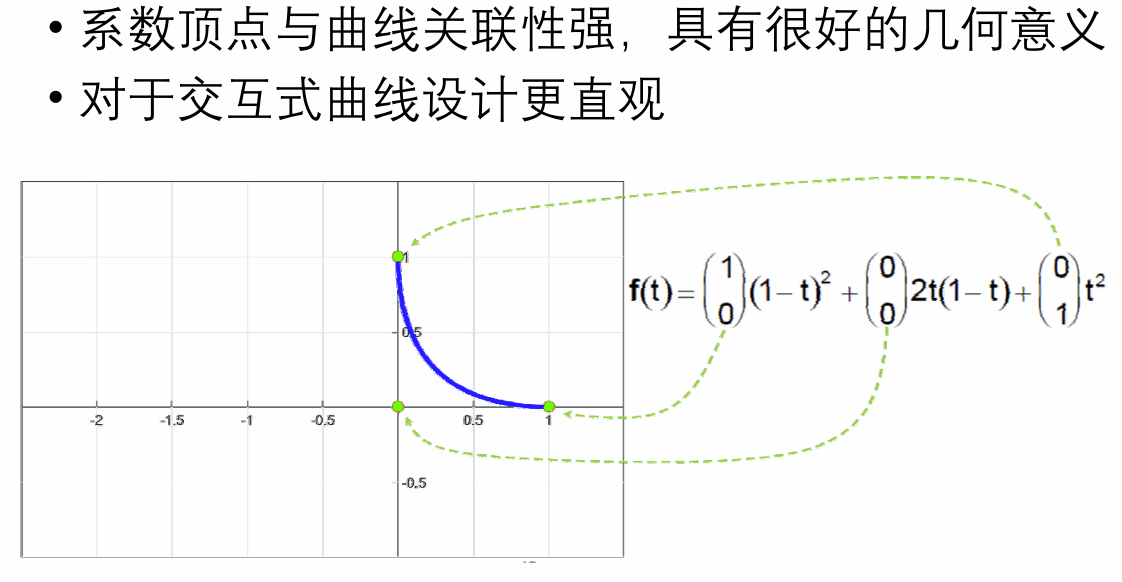
Bernstein基函数
n次Bernstein基函数B = {B0(n), B1(n), …, Bn(n)}
where the binomial coefficients are given by:
例子:
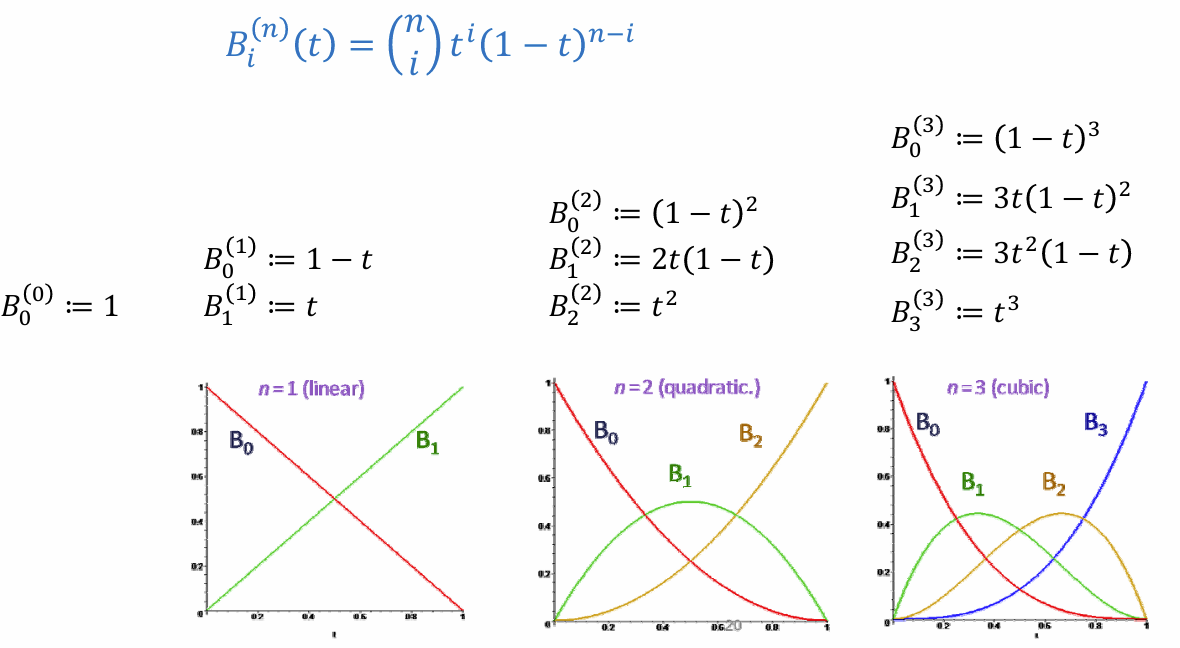
用Bernstein基函数所表达的曲线具有非常好的几何意义
Bezier曲线
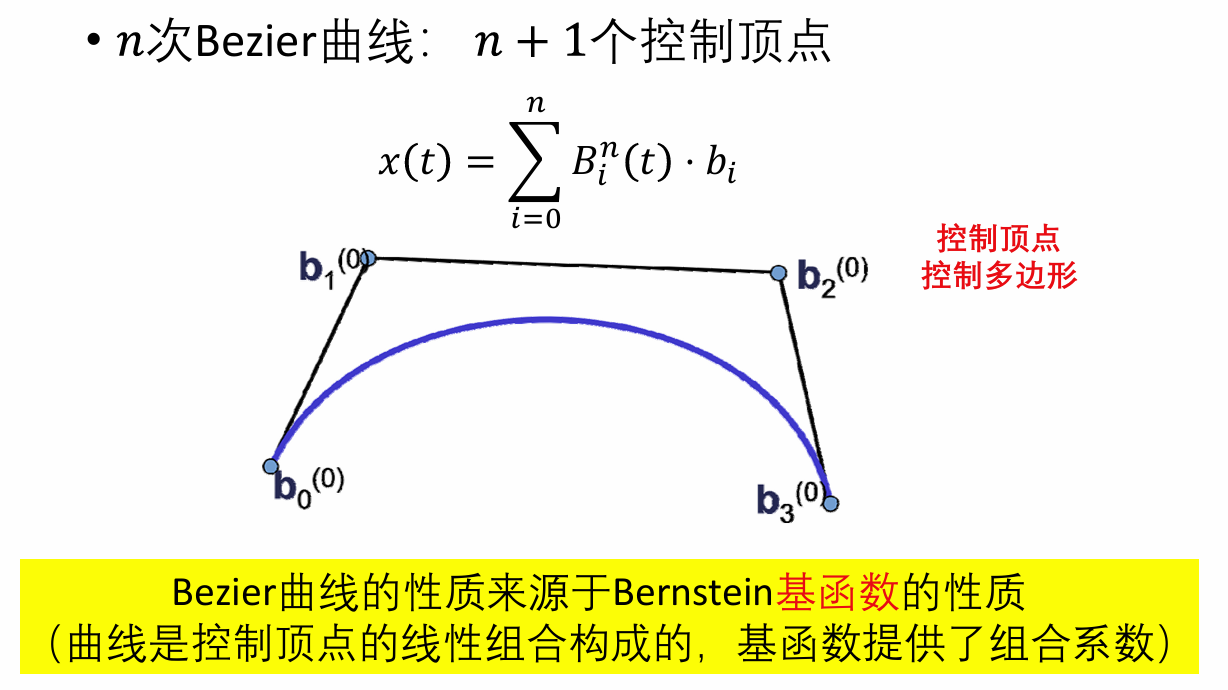
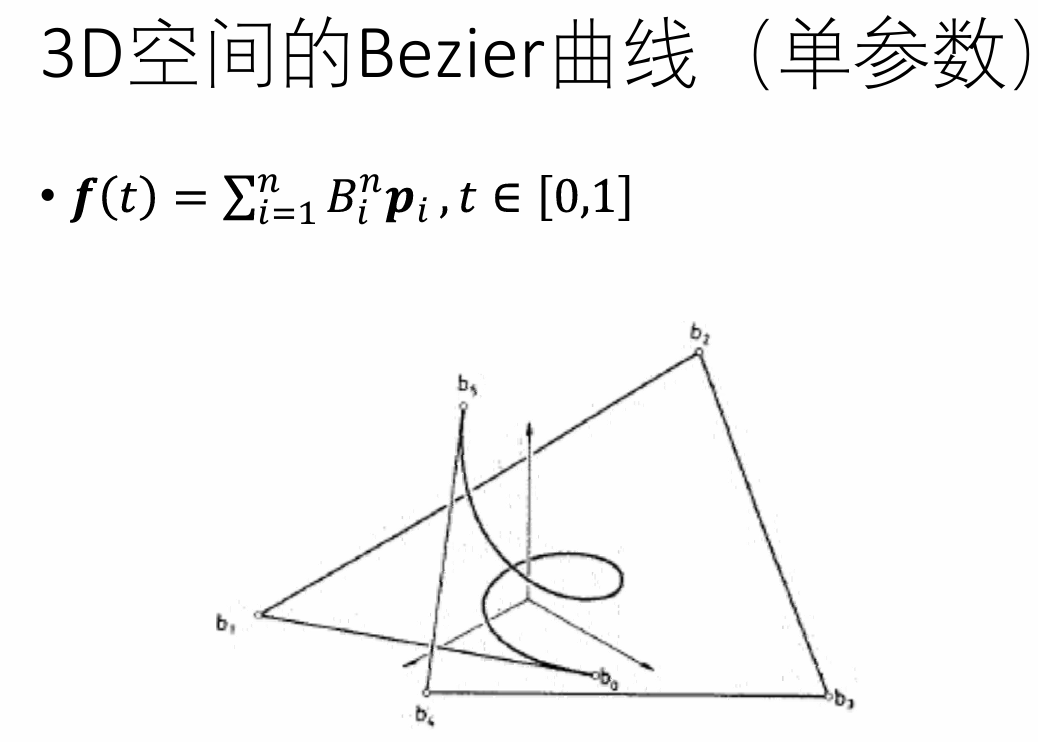
Bernstein基函数
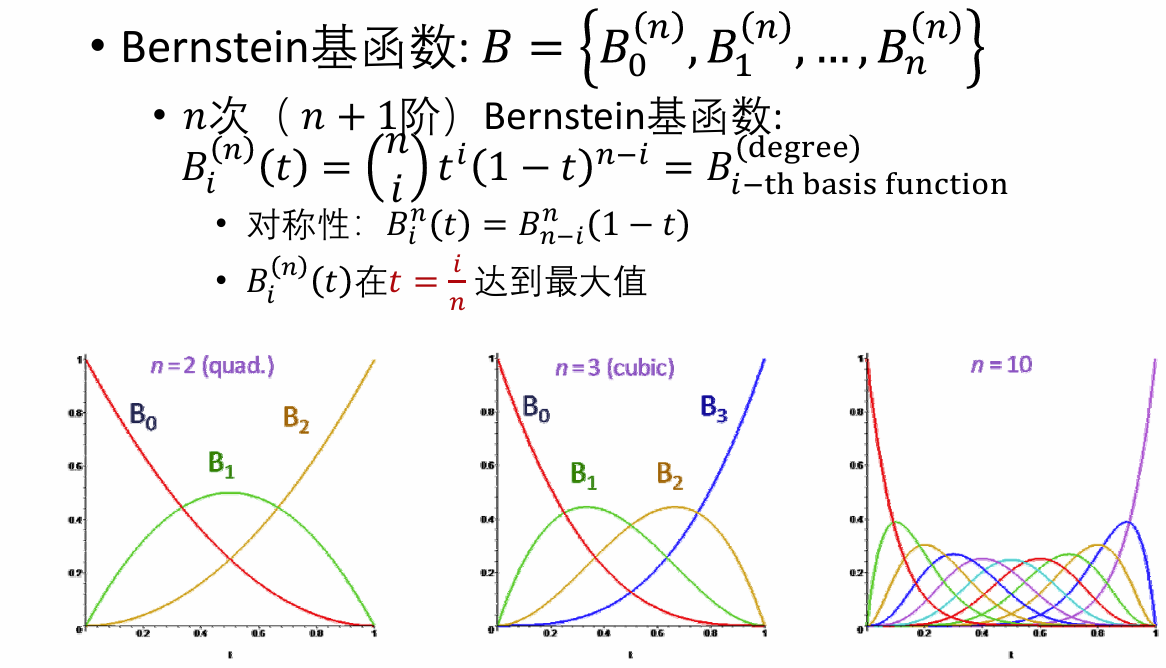
Bernstein基函数性质:
- 正性(非负性) + 权性 → Bezier曲线的凸包性
Bi(n)(t) ≥ 0, ∀t ∈ [0, 1]
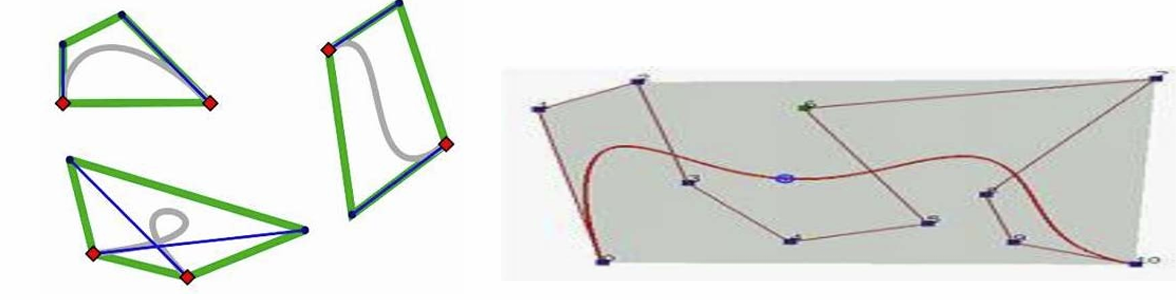
基性
B = {B0(n), B1(n), …, Bn(n)}是次数不高于n的多项式集合(空间)的一组基
与幂基可以相互线性表达:
递推公式
基函数的递推公式
- with
B00(t) = 1, Bin(t) = 0 for i ∉ {0, …, n}
- 由
- 可推导得到
高阶的基函数由2个低阶的基函数“升阶”得到(利于保持一些良好的性质)
端点插值性
- B0n(0) = 1, B1n(0) = ⋯ = Bnn(0) = 0
- B0n(1) = ⋯ = Bn − 1n(1) = 0, Bnn(1) = 1
- 可知Bezier曲线经过首末两个控制顶点p0, pn
导数

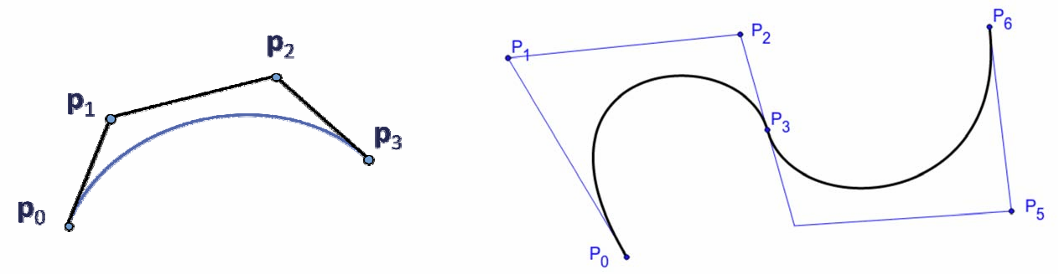
Bezier曲线的端点性质:
- 端点插值:
- f(0) = P0
- f(1) = Pn
- 端点的切线方向与边相同:
- f′(0) = n[P1 − P0]
- f′(1) = n[Pn − 1 − Pn]
- 端点的2阶(k)切线与3点(k+1)相关:
- f″(0) = n(n − 1)[P2 − 2P1 + P0]
- f″(1) = n(n − 1)[Pn − 2Pn − 1 + Pn − 2]
- 端点插值:
升阶
可知Bezier曲线的升阶:
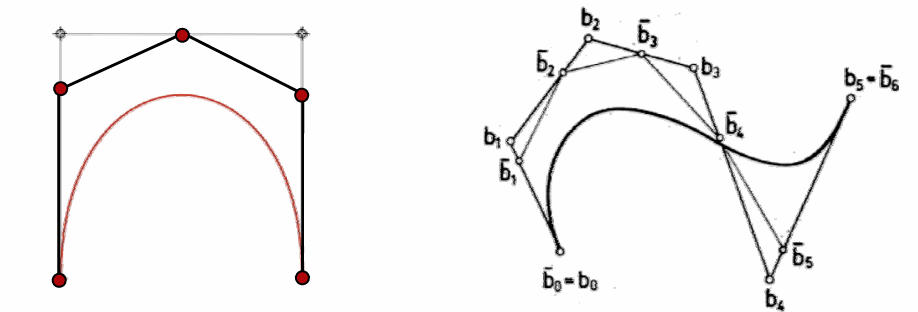
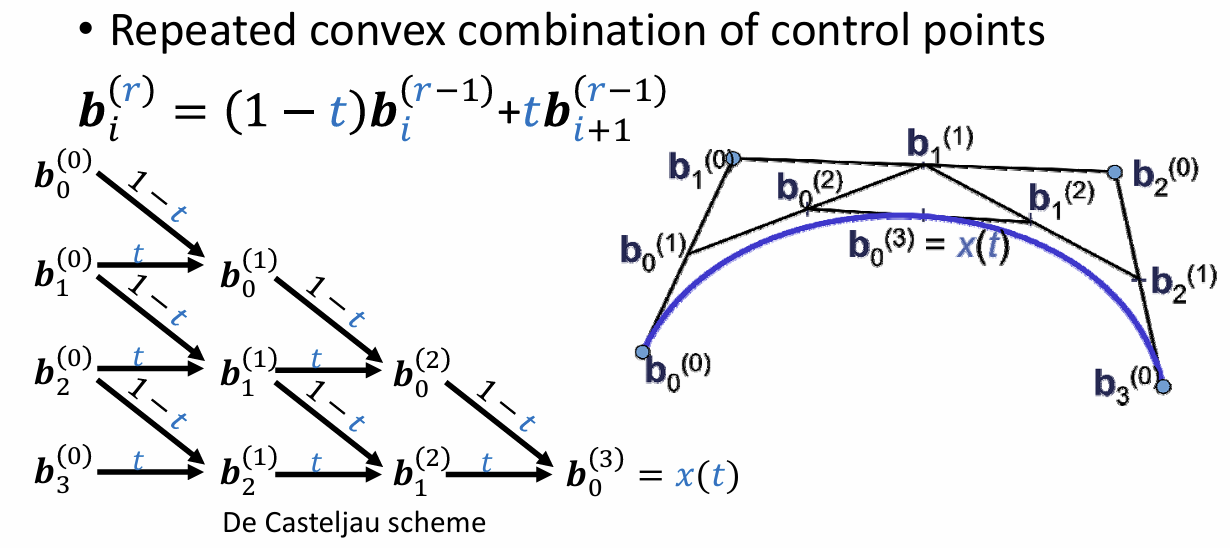
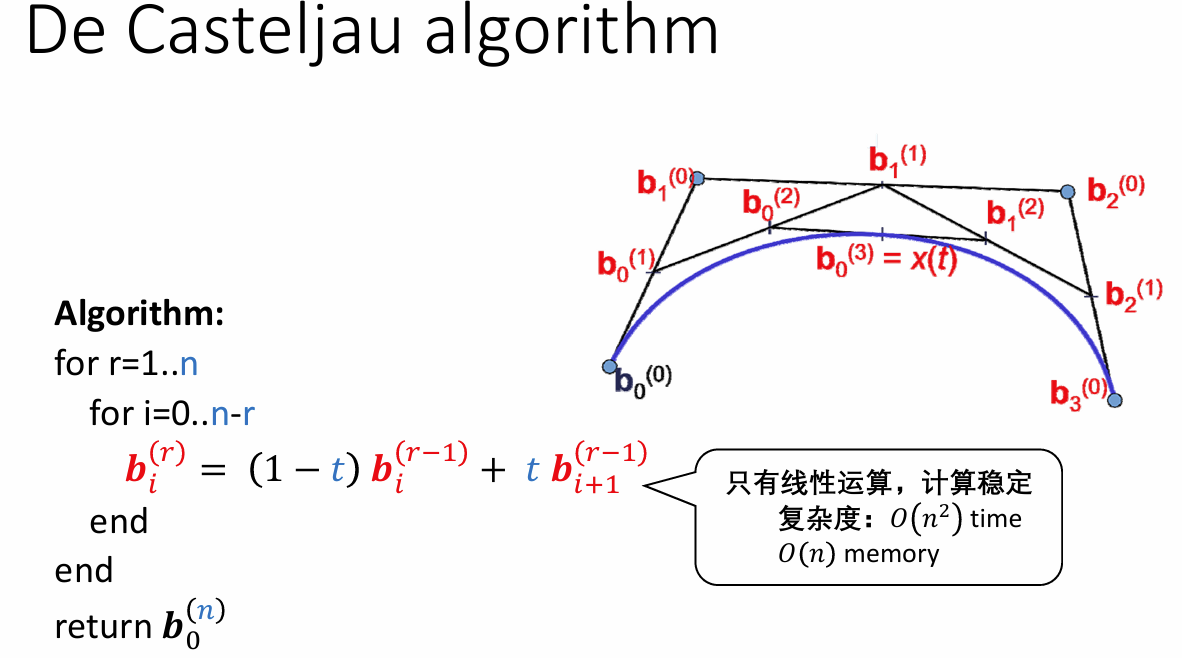
Bezier曲线的 de Casteljau算法
- 最后一条边一定与最终的曲线相切

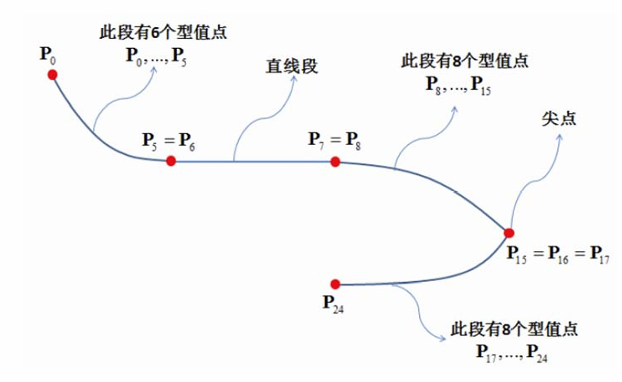
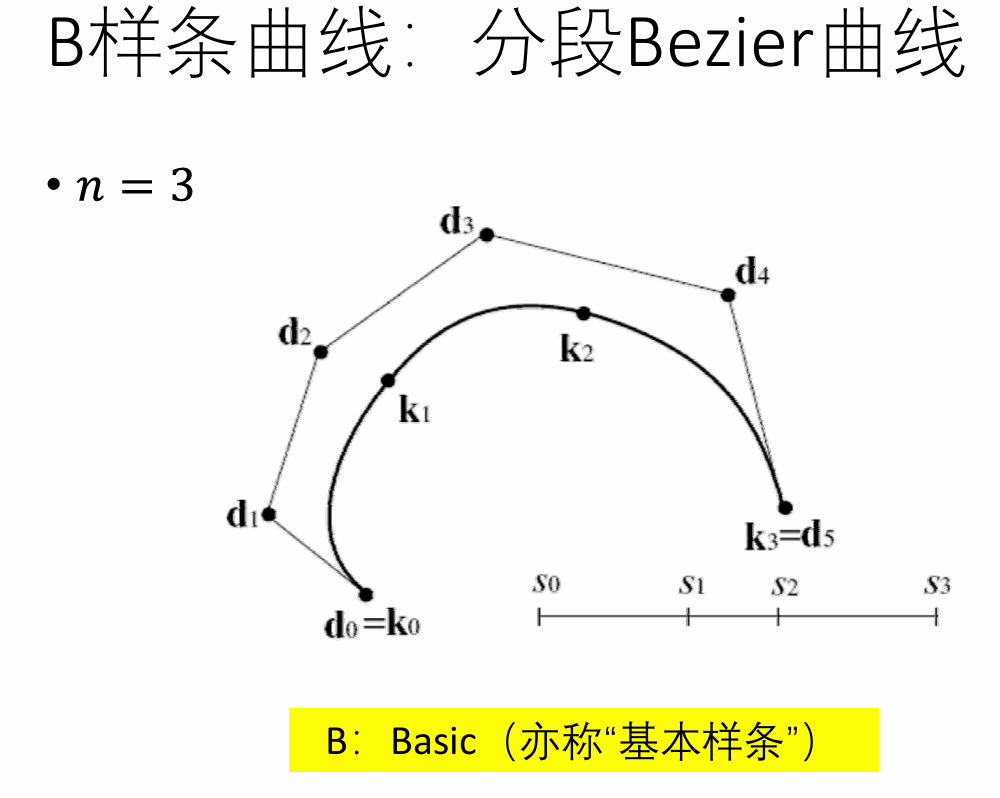
几何样条曲线
用分段Bezier曲线来插值型值点
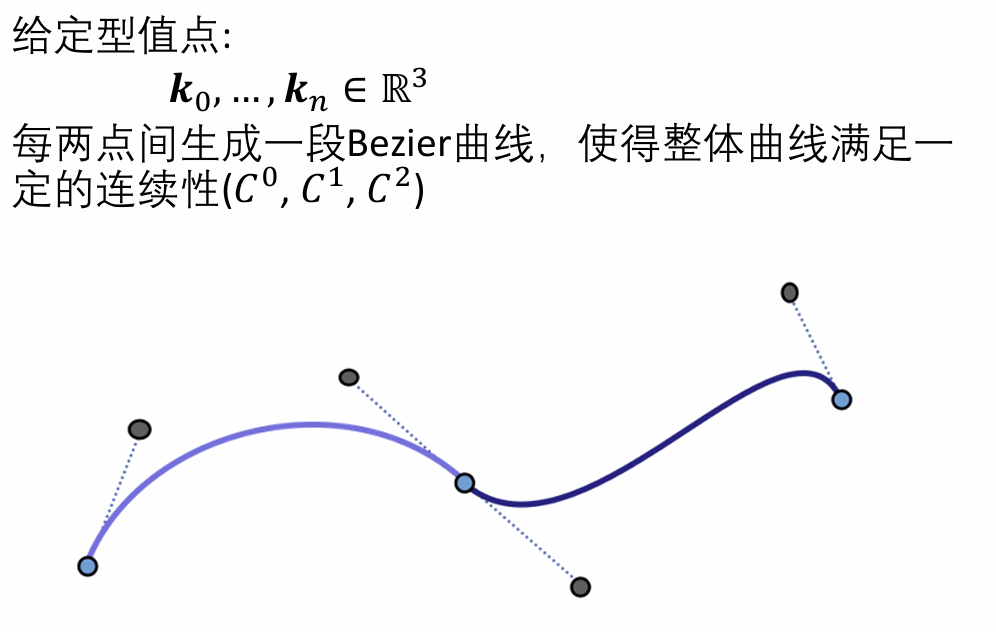
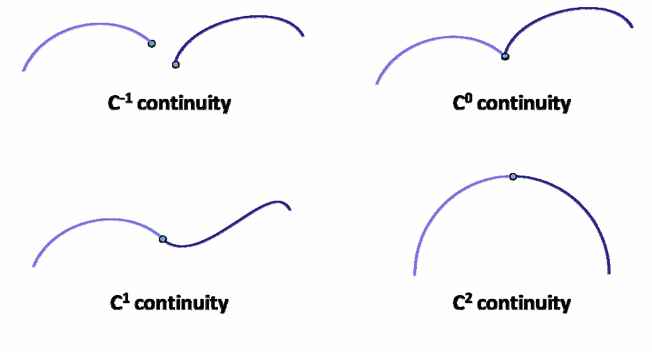
两Bezier曲线的拼接条件:
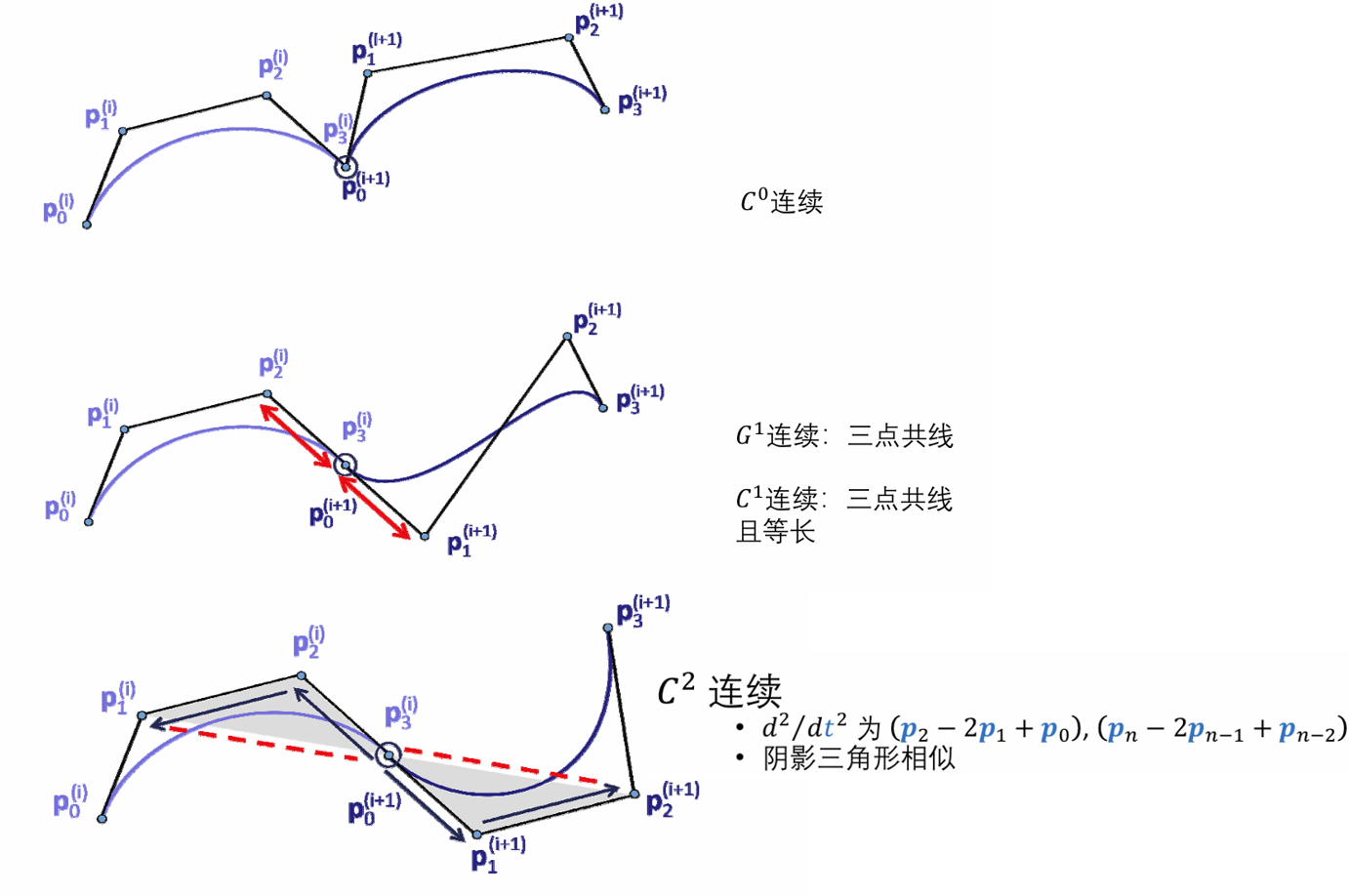
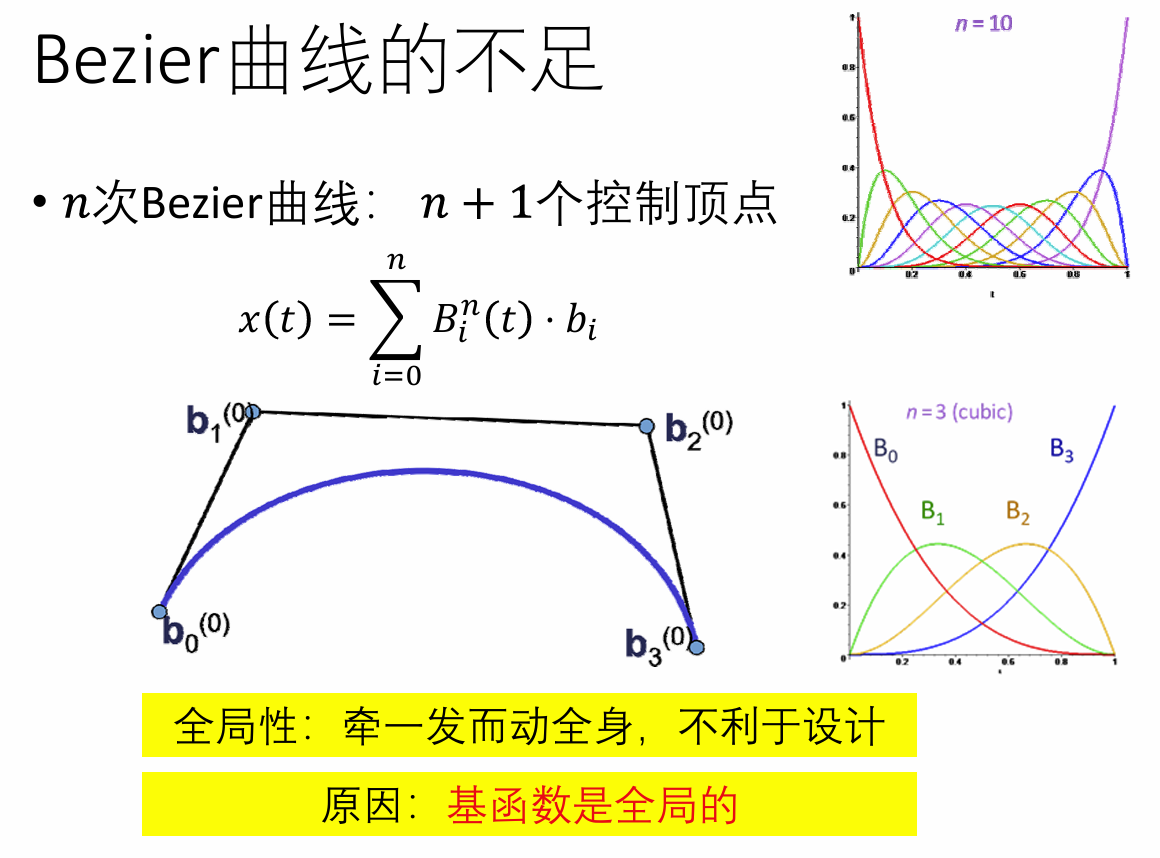
广义样条曲线
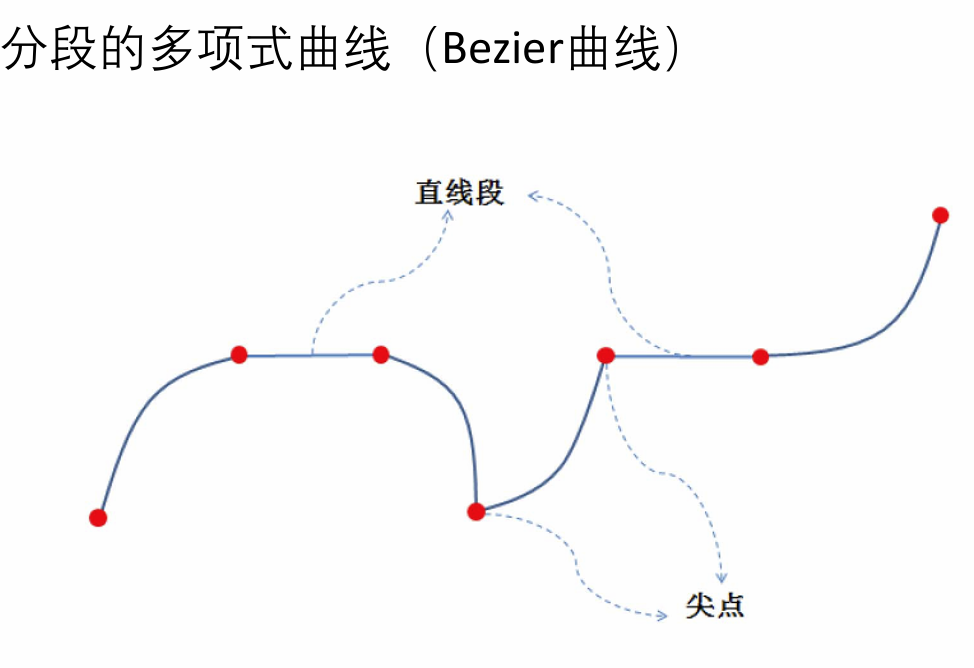
分段表达时具有局部性,如何形成一个统一表达?

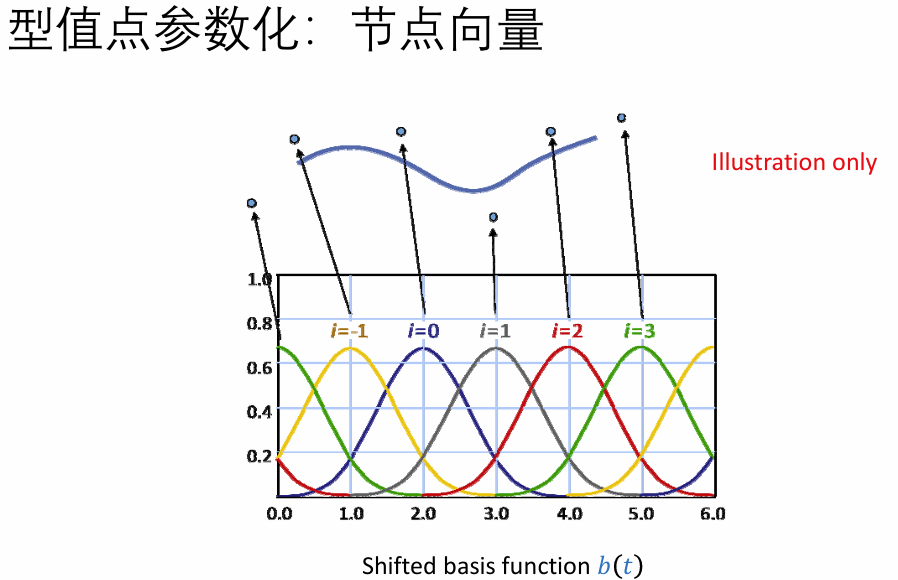
从Bernstein基函数的递推公式得到启发:
- 局部处处类似定义,由一个基函数平移得到
- 高阶的基函数由2个低阶的基函数“升阶”得到
关键思路:
构造一个基函数b(t),它存在以下性质:
b(t) 是 C2 连续的
b(t) 是分段多项式
b(t) 具有局部支撑
叠加平移的 b(t+i) 形成统一的分割
对所有 t,b(t) ≥ 0 b(t) ≥ 0
简而言之就是所有理想的性质都在基函数中体现,线性组合将继承这些性质。
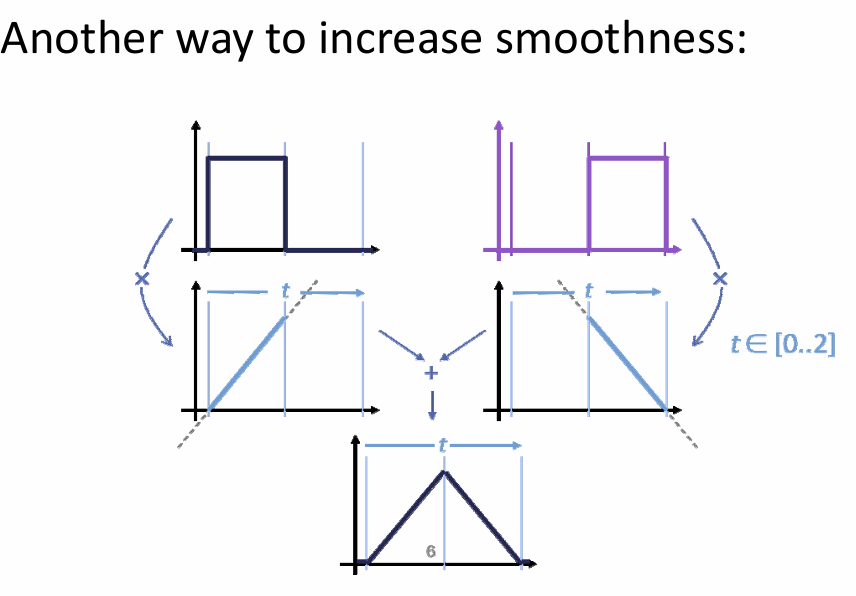
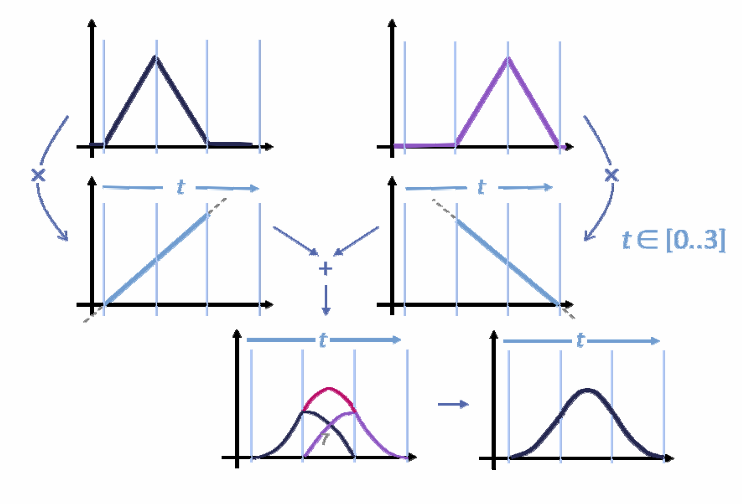
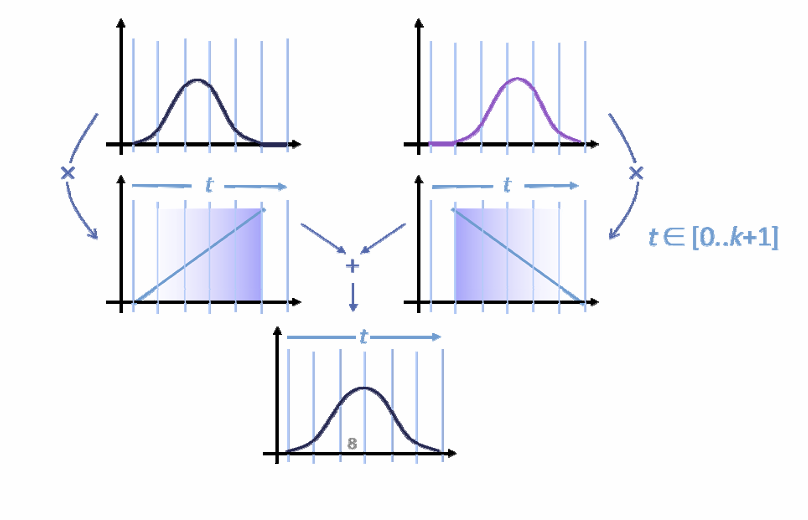
每次多一阶。
- 对于均匀节点:
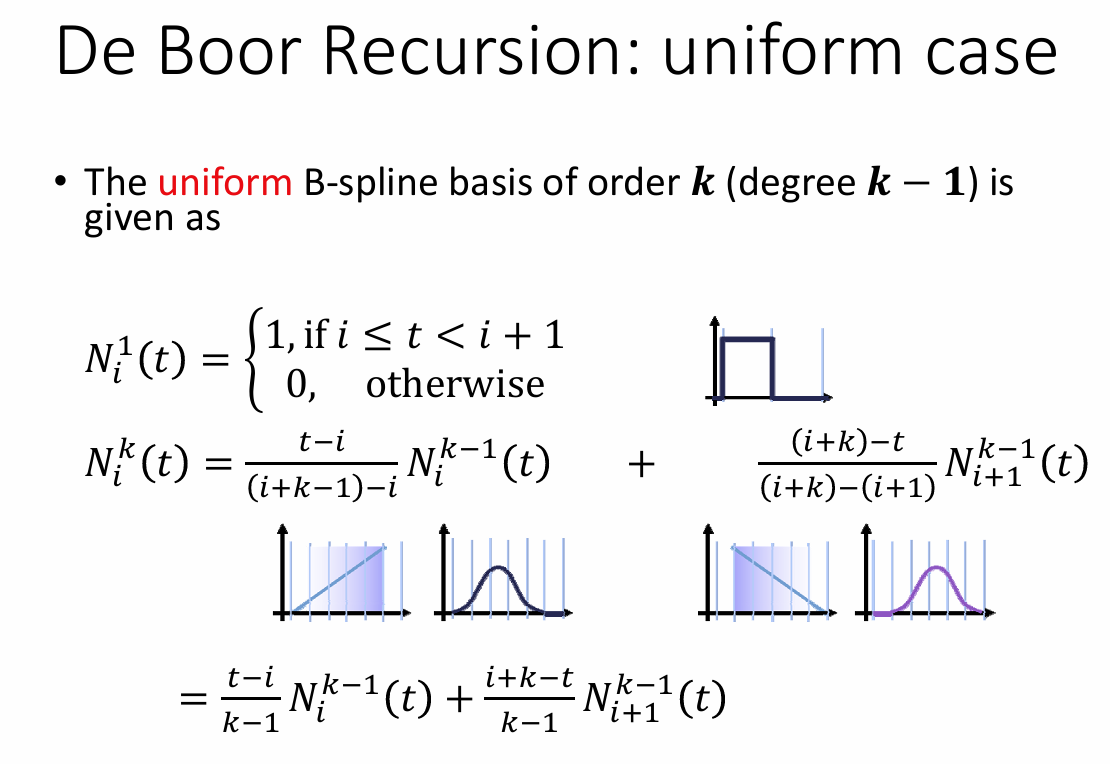
- 非均匀节点:

基函数的性质:
当 时 - 当t0 < t < ti或ti + k < t < tn + k时,Ni, k(t) = 0
当 时 所 有 基 函 数 的 和 - 对于ti ≤ tj ≤ ti + k,基函数Ni, k(t)连续的
- 区间[ti, ti + k]被称为Ni, k的支撑集
B样条曲线:
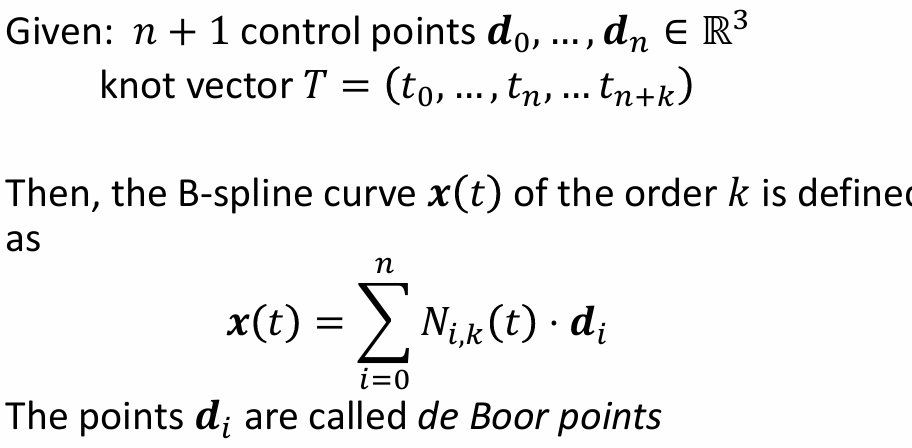
多重加权结点向量:
- 允许tk ≤ tk + 1 ≤ tk + 2
- 只要没有超过 k 个结点重合,递归定义就能正常工作
- 节点重合可以改变曲线的光滑性
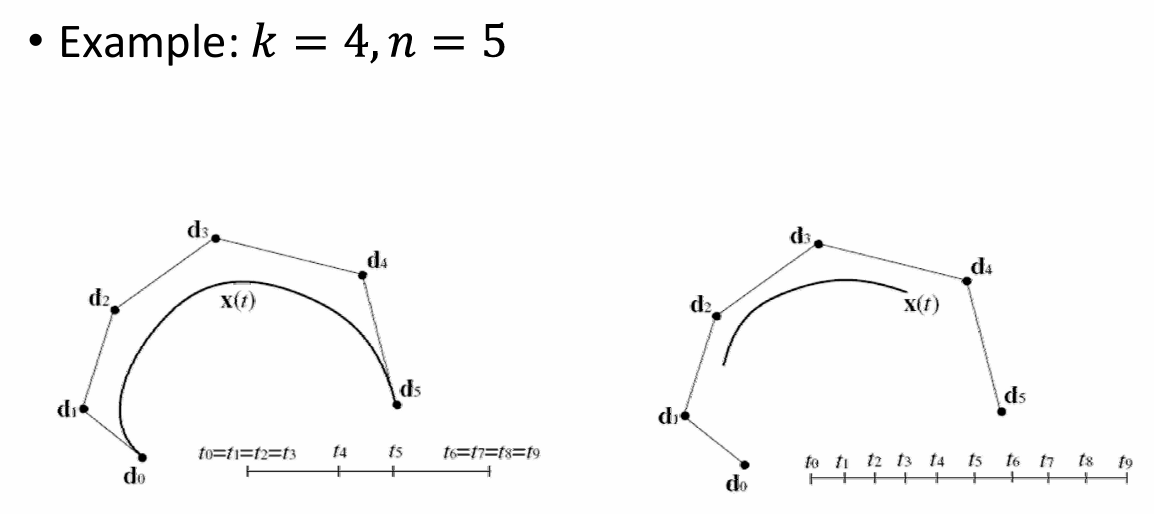
B样条函数实际上就是一个分段的多项式函数,但给出了一个统一的形式。
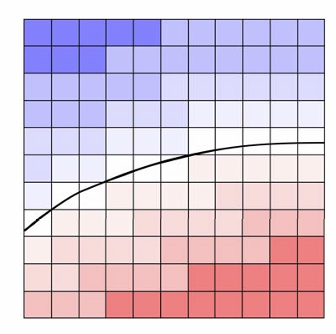
B样条的局部性:
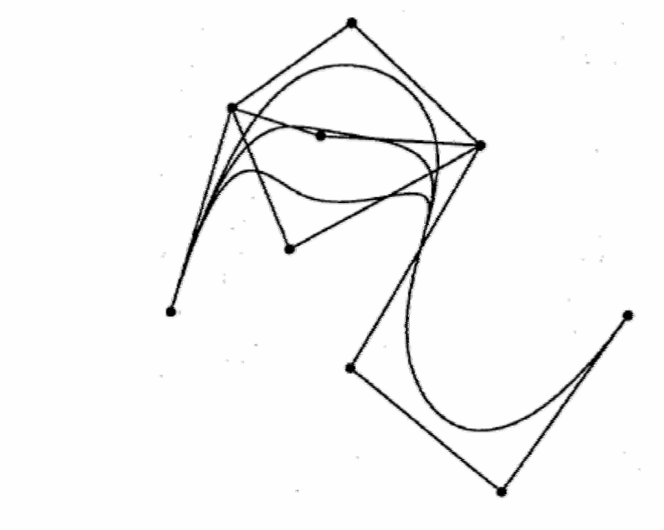
引申:在神经网络中把sigmod这种基函数变成局部基也能有这个性质,数据变化了只会影响一部分参数。
B样条的其它理论知识:
- B样条的许多性质:
- 局部凸包性:B样条曲线的局部修改只会影响曲线的局部部分。
- 变差缩减性:B样条曲线的平滑度可以通过调整结点向量来控制。
- 包络性:B样条曲线可以被其控制点的凸包所包围。
- 导数和积分的递推式:B样条曲线的导数和积分可以通过递推式计算。
- 几何作图:B样条曲线可以通过几何方法绘制。
- 重节点的B样条基函数及曲线
- Bezier样条曲线与B样条曲线的转换
- B样条插值方法