GAMES102-04-三次样条函数

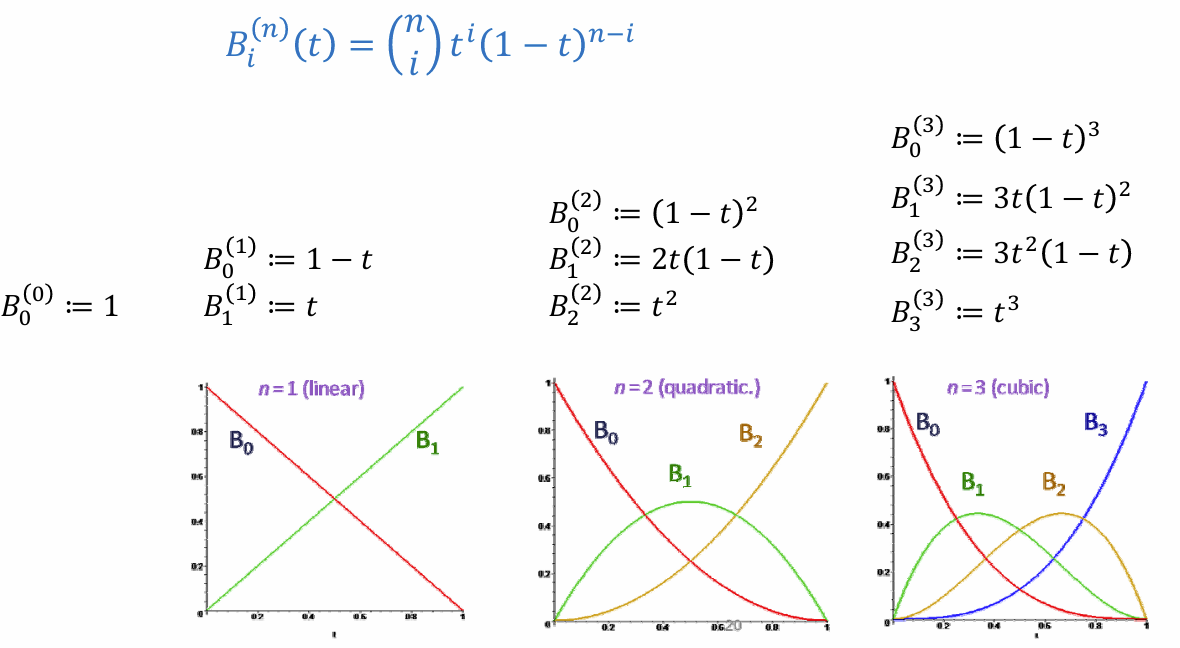
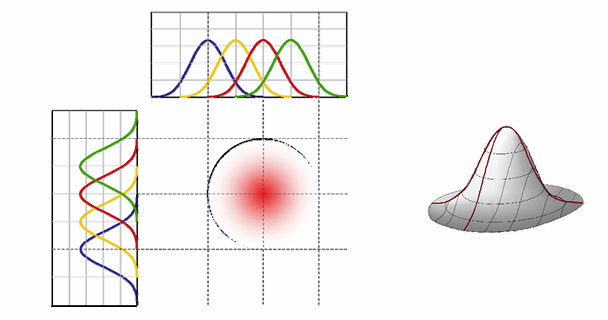
Lecture 04 Cubic Spline

样条和压铁：没有电脑之前设计师的画图设计方法

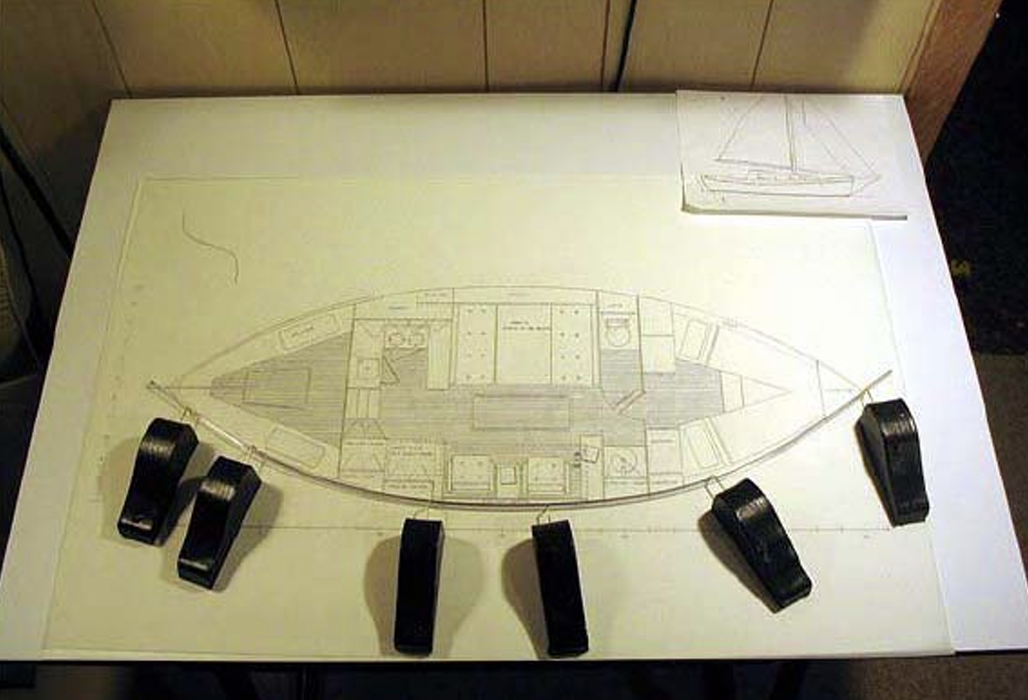
在产品初始设计阶段，描述其外形的曲线或曲面常常只有大致形状或只知道它通过一些空间点列（称为型值点），这类没有数学表达式的曲线或曲面称为自由曲线或自由曲面(Free form curve/surface)

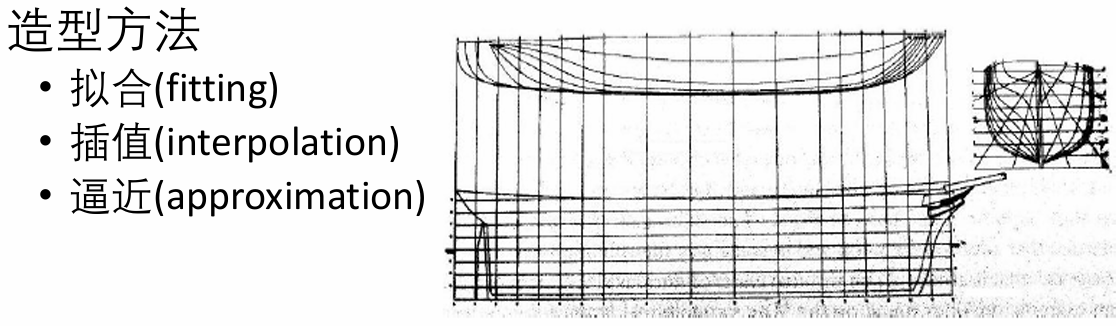
三次样条的来源：

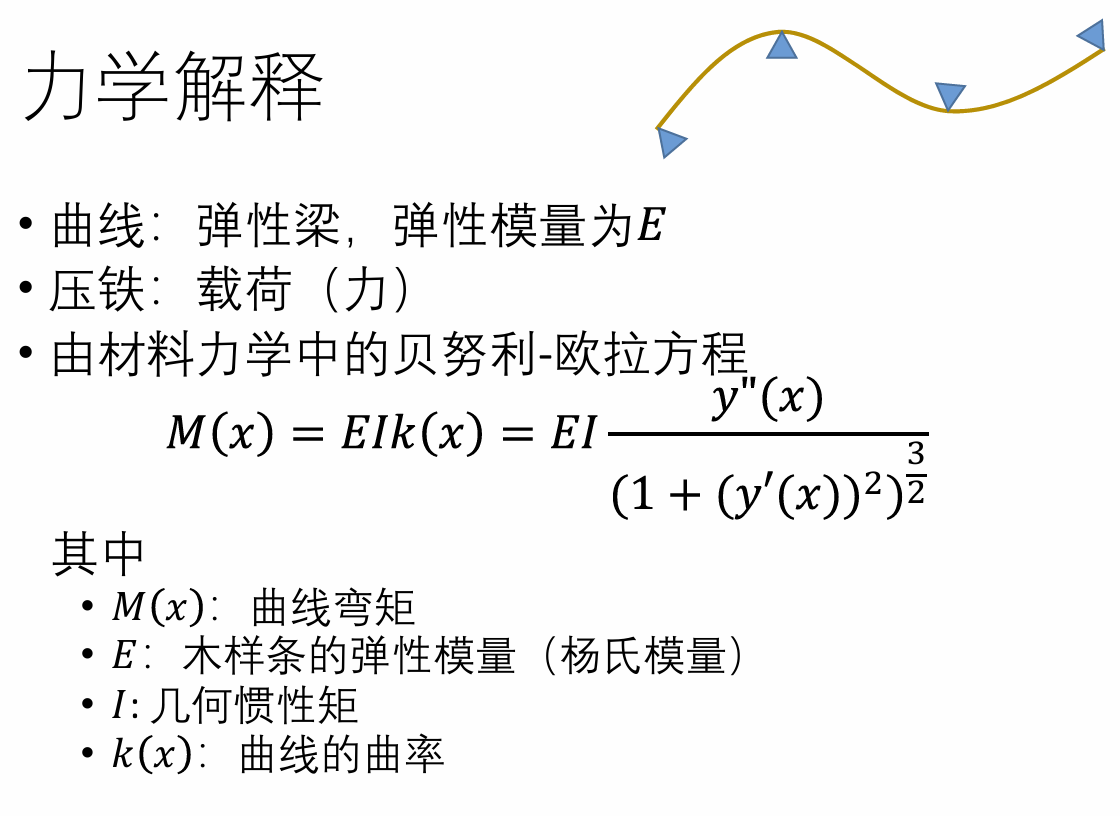
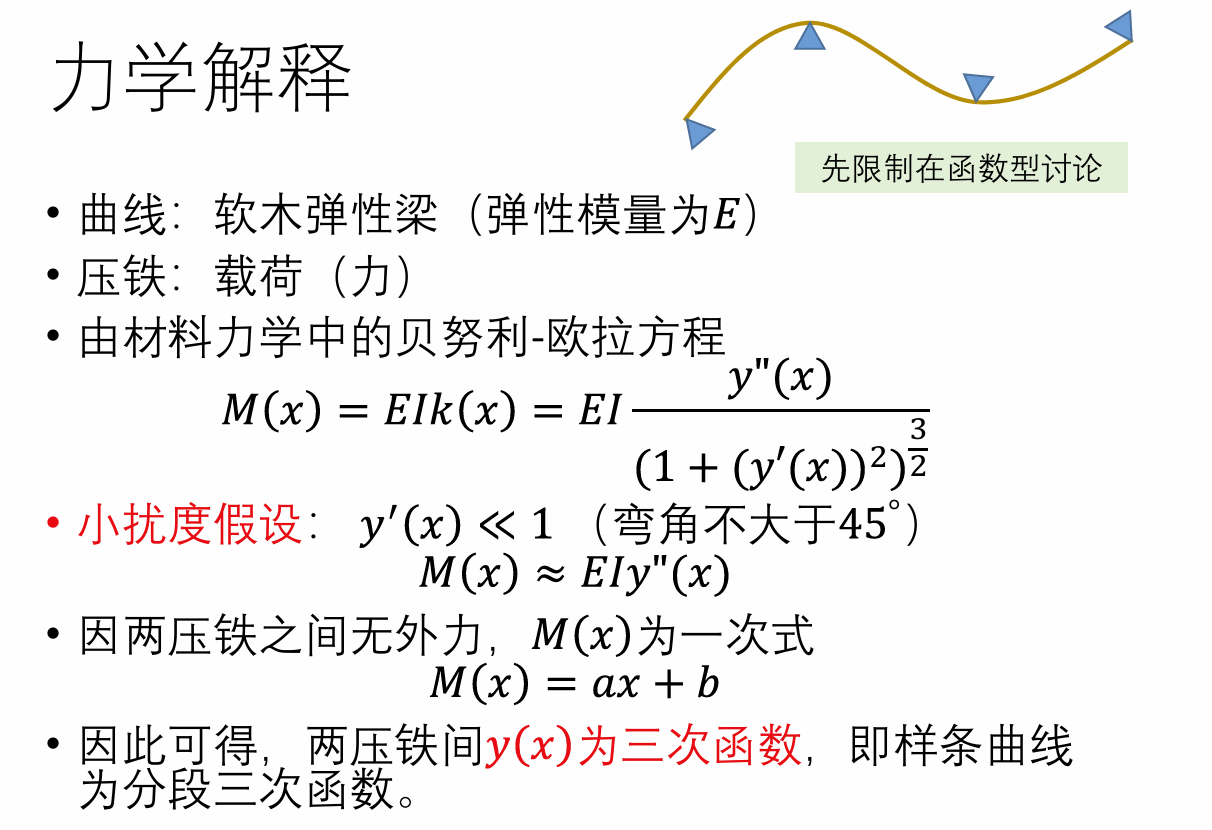
数学性质上：

• 分段三次多项式的好处：
  • 二次多项式无法表达拐点，不够自由
  • 高次（四次及以上）多项式拐点多，次数若较高则计算易出现较大误差

三次样条曲线

求解思路：

这个额外条件即为曲线首尾。

推导过程：

• 方法一：三弯矩方程组
  • 根据3次样条插值函数的定义
  • 引入中间变量节点处的二阶导数值Mⁱ（弯矩）
  • 把每段y''i(x)表达为Mⁱ和Mⁱ⁺¹的线性插值
  • 则yi(x)为包含Mi的三次多项式
  • 再根据拼接条件列出等式，加上两个边界条件可以得到线性方程组
  • 方程组为对称的、三对角的、对角占优的，称为三弯矩方程组
  • 方程组系数矩阵满秩，有唯一解
  • 可用追赶法求解三弯矩方程组

边界条件：

• 自由端：指定曲线在两个端点处的二阶导数值
  • 特别地，两个端点的二阶导数值指定为0时称为自然三次样条
• 夹持端：指定曲线在两个端点处的一阶导数值
• 其他：
  • 抛物端：首末两段为抛物线
  • 周期端
  • 混合边界条件
• 方法二：三转角方程组
  • 根据3次样条插值函数的定义
  • 引入中间变量：节点处的一阶导数值Mⁱ（转角）
  • …（推导过程类似）
  • 最后加上2个边界条件，构成线性方程组
  • 方程组为对称的、三对角的、对角占优的，称为三转角方程组
  • 方程组系数矩阵满秩，有唯 一解
  • 同样可用追赶法求解三转角方程组

三弯矩方程组/三转角方程组的共同点：

• 三对角矩阵
• 主对角占优
• 有唯一解
• 追赶法求解

简化的计算技巧（通用技巧）：

• Hermite型插值多项式
  • 两点及其一阶导数（切线）
• Lidstone型插值多项式
  • 两点及其二阶导数（曲率）
• 好处：在给定两个端点及其导数情况下，可直接写出函数的表达形式

三次基样条：

样条函数的局限性：

• 须有小扰度假定
• 不能处理多值问题
• 不能很好表达空间曲线
• 不具有坐标不变性（几何不变性）

三次参数样条曲线：

• 3个坐标分量x, y, z分别是参数t的三次样条函数
• 对型值点做参数化
• 对3个坐标分量分别处理

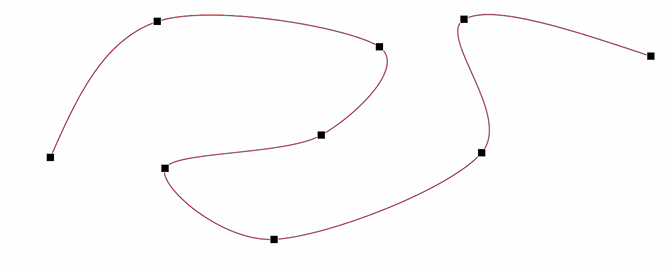
参数连续性：不挨着 --- 挨着 --- 一阶导一致 --- 两阶导一致

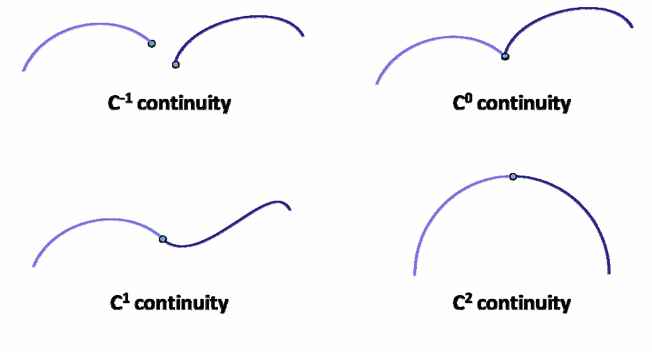
参数连续性过于严格，在几何设计中不太直观

几何连续性

定义：设 是给定的曲线。

若存在一个参数变换

使得 且

则称曲线 是 n 阶几何连续的曲线

记为 或

性质：

• 条件 保证了曲线上无奇点；
• 几何连续性与参数选取无关，是曲线本身固有的几何性质；
• 的条件比 的宽，曲线类型更多；

几何连续性的具体形式：

𝐺⁰：表示两曲线有公共的连接端点，与𝐶⁰的条件一致

𝐺¹：两曲线在连接点处有公共的切线，即切线方向连续

𝐺²：两曲线在连接点处有公共的曲率圆，即曲率连续

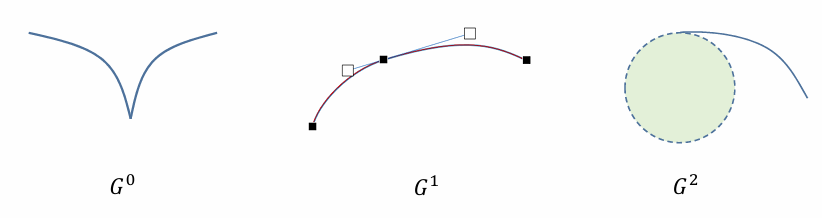
参数连续性和几何连续性

参数连续性：

• C0, C1, C2... 连续性
• 判定在这条曲线上移动的粒子是否具有平滑的轨迹（位置、速度、加速度...）
• 依赖于参数化
• 适用于动画（物体运动、摄像机路径）

几何连续性：

• 判定曲线本身是否平滑
• 独立于参数化
• 更适用于建模（曲线设计）