GAMES102-03-参数曲线拟合

Lecture 03 Curve Fitting

一元（单变量）函数拟合：

• 线性问题：解线性方程或线性方程组
• 非线性问题：
  • 凸问题：有理论保证
  • 非凸问题：难，需要数值求解。
    • 用梯度下降法、牛顿法、拟牛顿法等
    • 须选择合适初值、步长等
    • 一般要根据具体的优化问题形式及特点来设计合适的优化方法

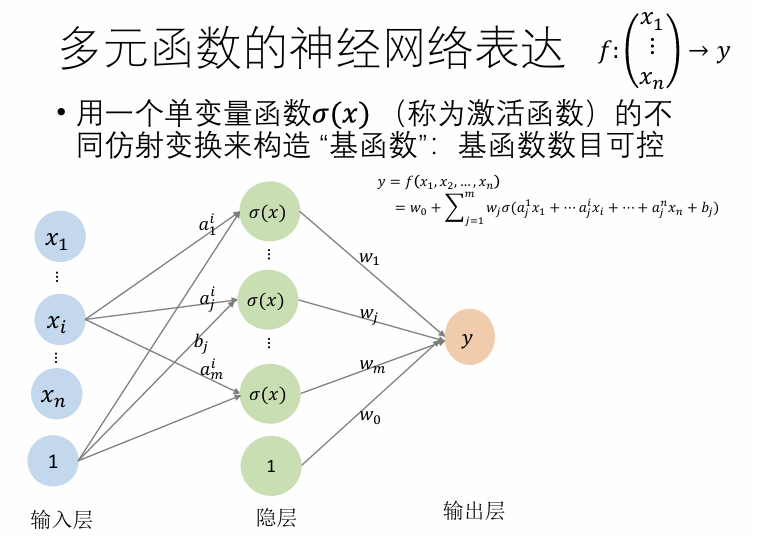
多元函数：多个变量的函数

y = f(x₁, x₂, ..., x_n)

二元函数的基函数构造：张量积形式，即用两个一元函数的基函数的相互乘积来定义。

例如二次二元多项式函数的基函数为：

{1, x, y, x², xy, y²}

三元张量积函数：

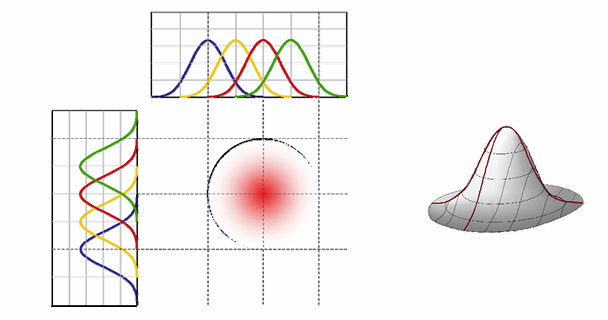
多元函数的张量积定义：

• 优点：定义简单，多个一元基函数的成绩形式
• 不足：随着维数增加，基函数个数急剧增加，导致变量急剧增加（求解系统规模急剧增加，求解代价大）
• 另一种方法：神经网络，数学上可以理解成一层神经元就是一个拟合函数

向量值函数：多个应变量

看成多个单变量函数，各个函数独立无关

• 一般会用同样的基函数（共享基函数）

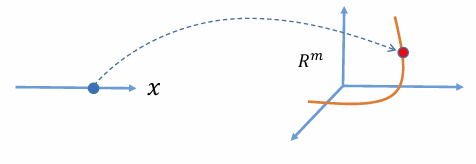
f : R¹ → R^m

• 几何解释：
  • 一个实数𝑥∈一维空间映射到𝑚维空间𝑅的一个点，轨迹构成𝑅的一条“曲线”
  • 本质维度为1
  • 

特例：平面参数曲线

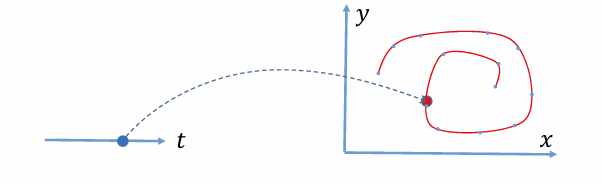
f : R¹ → R²

几何解释：

• 一个曲线由一个变量参数t决定，也称为单参数曲线
• 参数t可看成该曲线的“时间”变量
• 可灵活表达非函数型的曲线（任意曲线）

特例：空间参数曲线

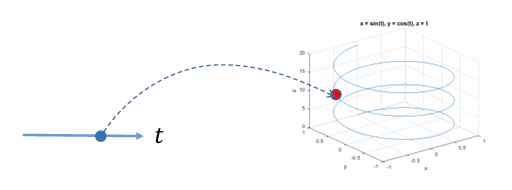
f : R¹ → R³

几何解释

• 一个曲线由一个变量参数t决定，也称为单参数曲线
• 参数t可看成该曲线的“时间”变量
• 可灵活表达非函数型的曲线（任意曲线）

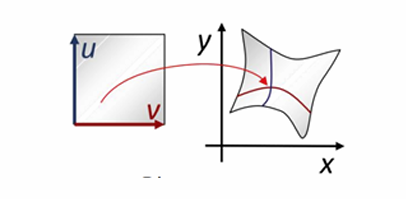
特例：参数曲面

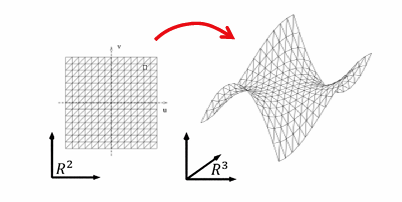
f : R² → R³

几何解释：

• 一个曲线由两个变量参数(u,v)决定，也称为双参数曲面（也叫流形）
• 本质维度是2
• 可灵活表达非函数型的任意曲面

特例：二维映射

f : R² → R²

几何解释：

• 二维区域之间的映射
• 可看成特殊的曲面（第三个维度始终为0）
• 应用：图像变形

特例：三维映射

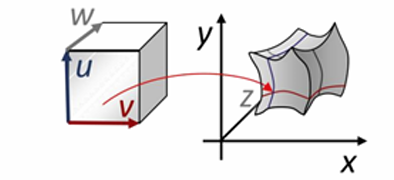
f : R³ → R³

几何解释：

• 三维体区域之间的映射
• 应用：体形变、体参数化

特例：降维映射（低维投影）

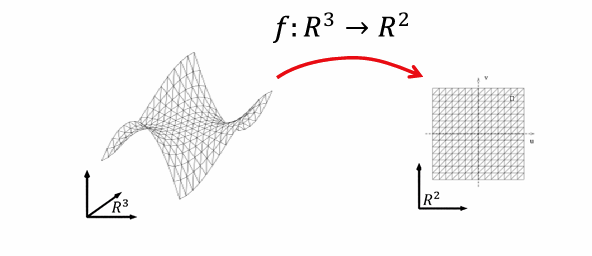
• 降维映射一般有信息丢失
• 丢失的信息大部分情况下不可逆，即无法恢复

一般映射

f : Rⁿ → R^m

• 如果 n＜m，为低维到高维的映射（高维的超曲面，n维流形曲面），本征维度为n。
• 如果n＞m，为降维映射，一般信息有损失。如果n维空间中的点集刚好位于一个𝑚 维（或小于𝑚 ）的流形上，则映射可能是无损的，即可以被恢复的。

低维空间之间的函数：

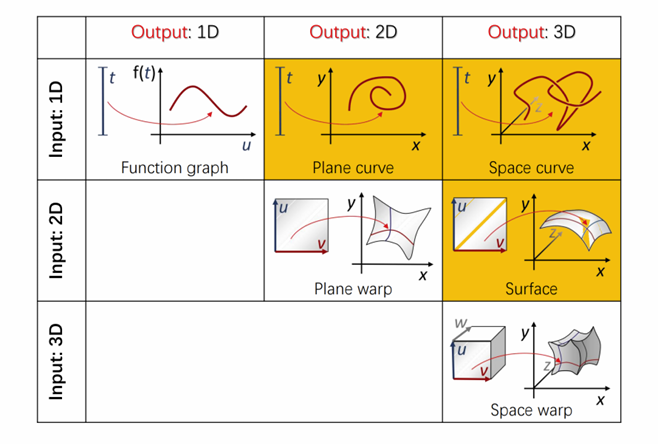
曲线拟合问题：

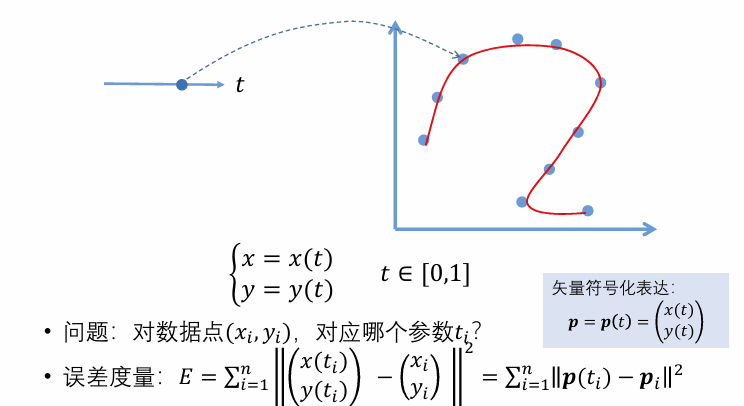
参数化问题：

• 求数据点所对应的参数（找ti）：一个降维的问题

点列的参数化方式：

均匀参数化：直接映射到t轴

t_i + 1 − t_i = const

eg.t_i = i

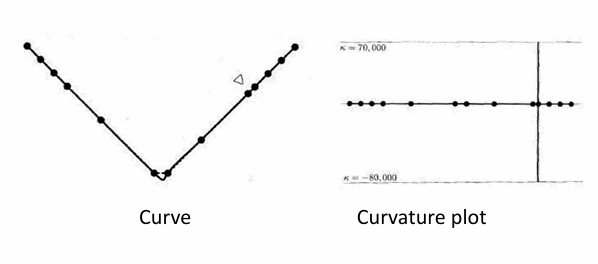
弦长参数化：映射到t轴并根据弦长拉伸

t_i + 1 − t_i = ||κ_i + 1 − κ_i||

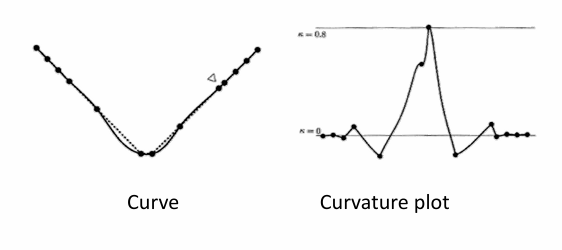
中心参数化：

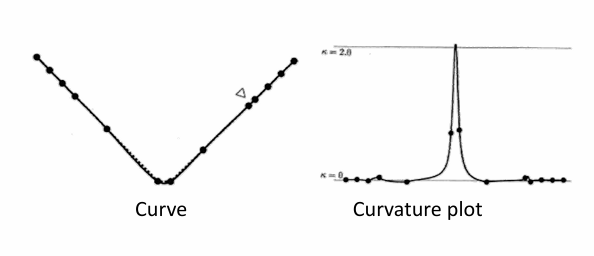
另一个例子：

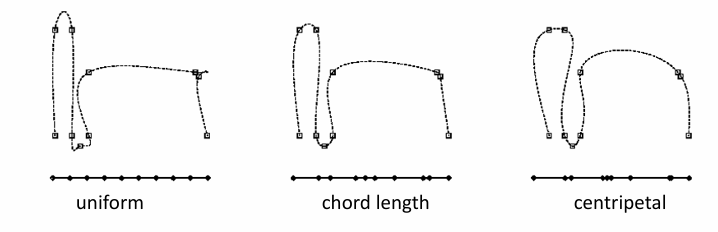
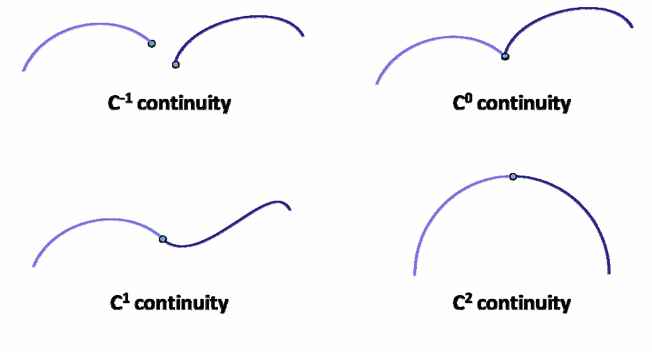
点的参数化对曲线拟合的影响很大，需要好的参数化

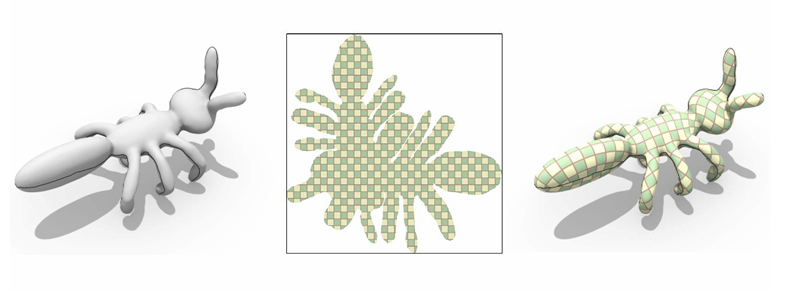
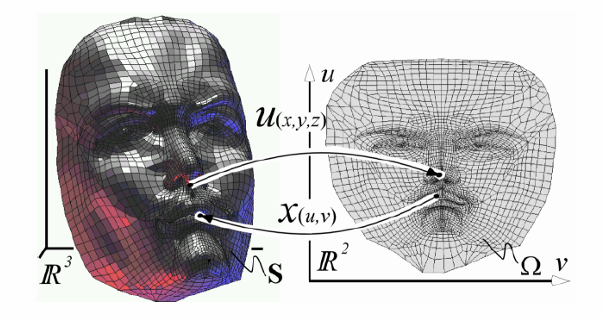
曲面参数化

三维的点找二维的参数：一个降维的问题

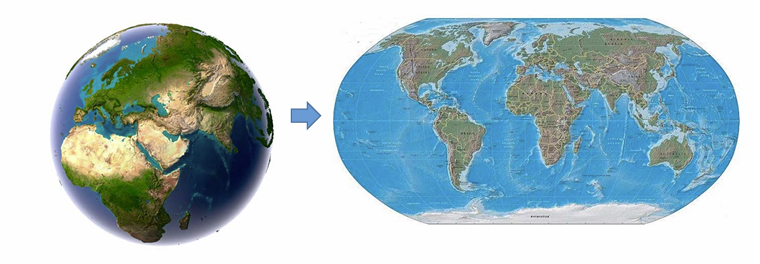
可展曲面：可以保长变换到平面中去，即可以被弯曲（非拉伸、收缩、皱褶或撕裂）而展开成一片平面。可展曲面是一种特殊的曲面，在微分几何中定义为在其上每一点处高斯曲率为零的曲面。

应用：

• 地图绘制（地理学）

• 纹理映射（UV图）