Lecture 02 Data Fitting
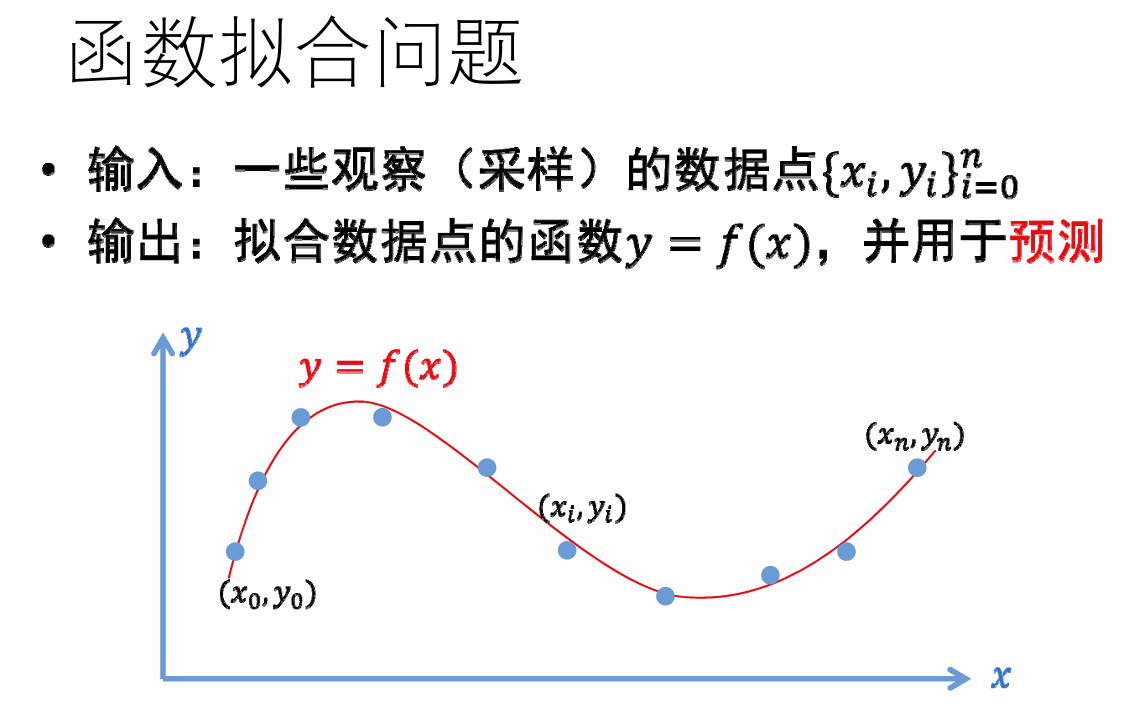
拟合函数的好坏:
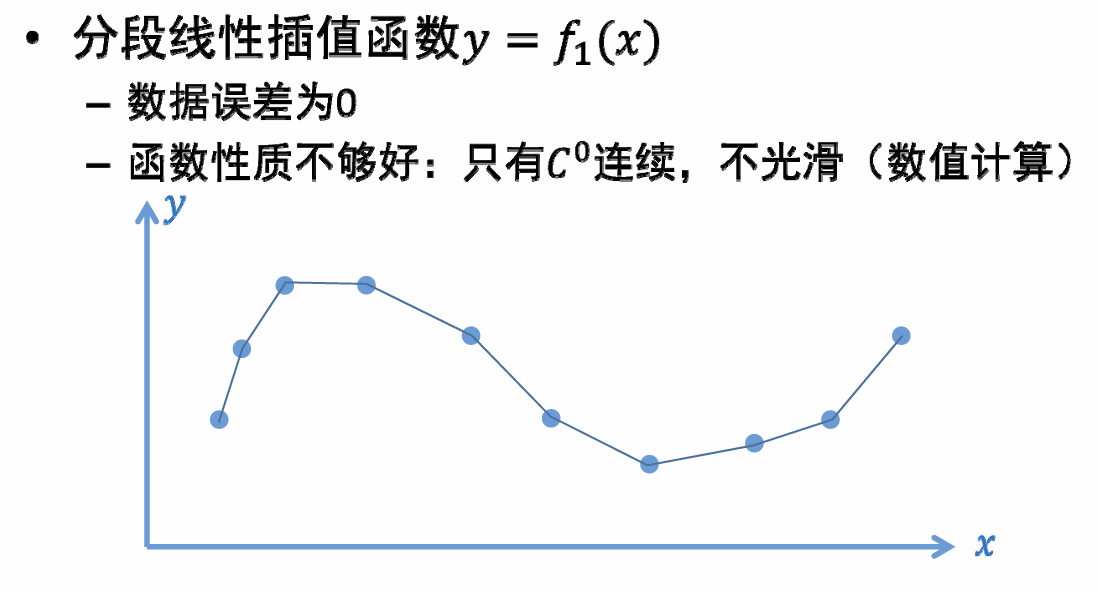
- 分段插值函数:
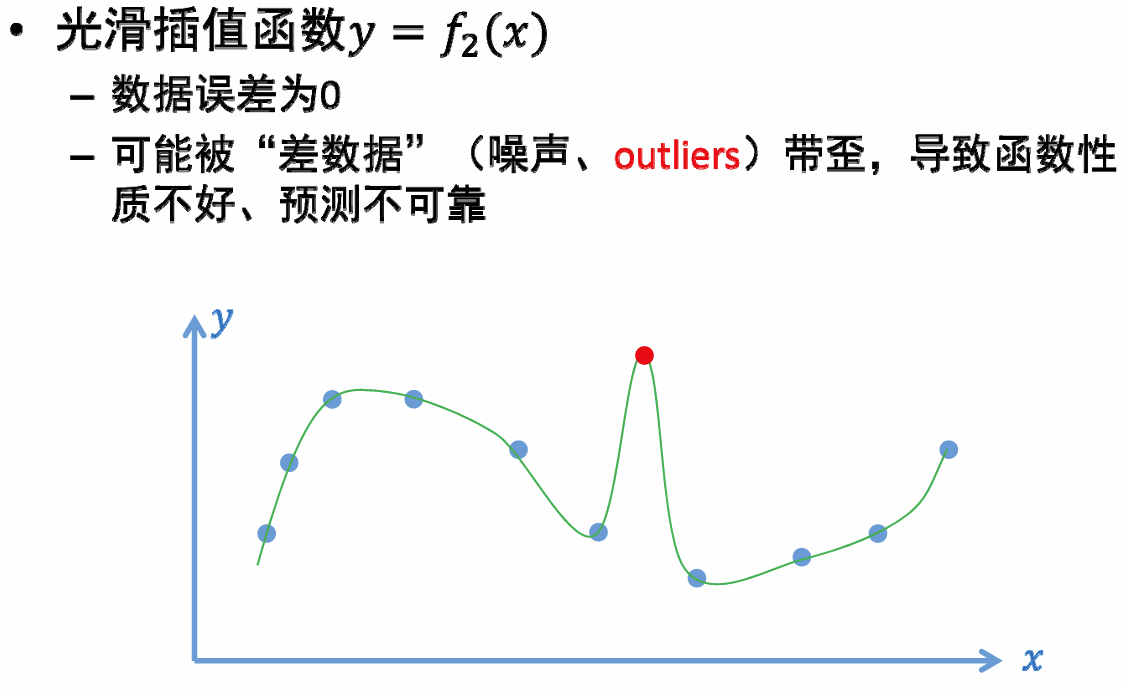
- 光滑插值函数:
- 逼近拟合函数:
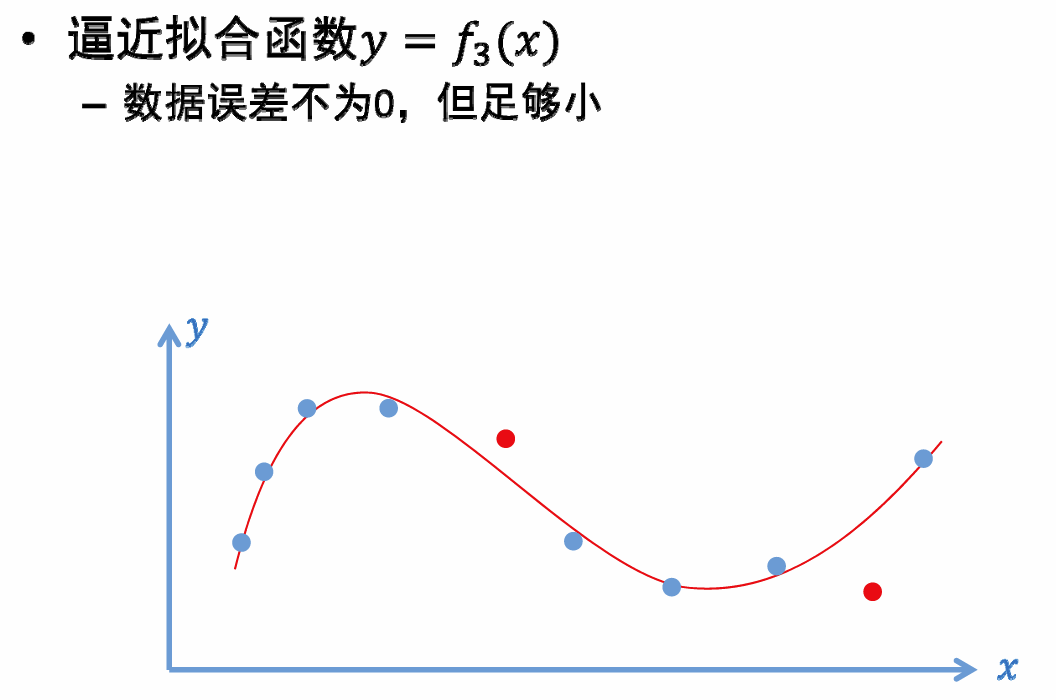
放在一起:拟合函数不唯一
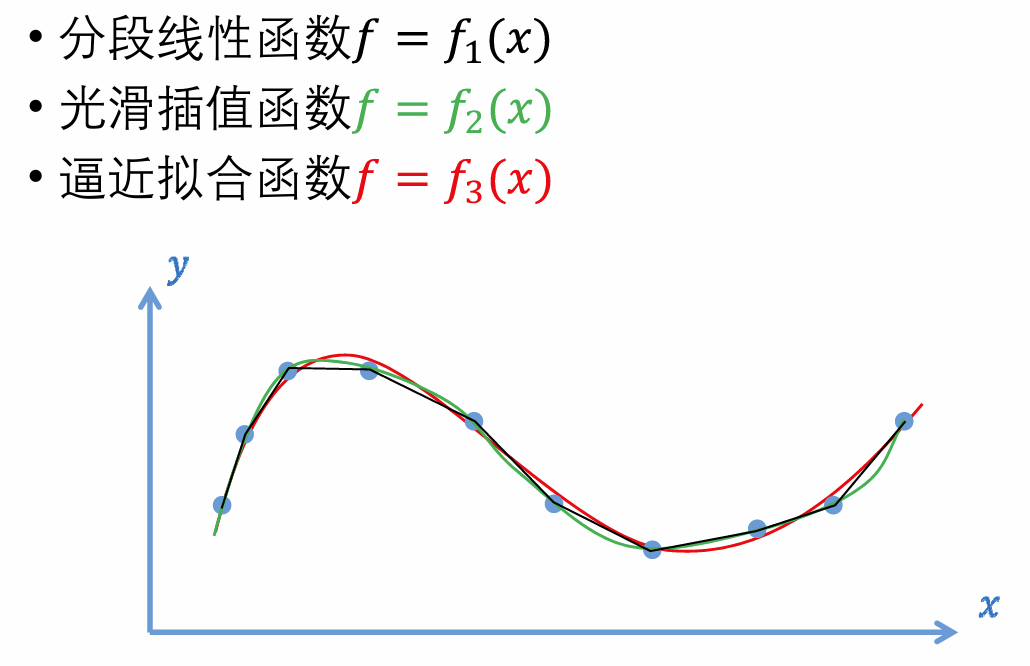
所以求拟合函数是一个应用驱动的过程,和领域强相关。
一般会把求解变量设置成基函数的组合系数,优化模型误差函数设置成误差项+正则项。
求解过程就是求解误差函数的驻点(导数为0处),即和系数有关的方程组,如果方程组是欠定的(有无穷多解的情况),则需要修正模型(例如加正则项或修改模型)。
多项式插值
多项式插值定理:若xi两两不同,则对任意给定的yi,存在唯一的次数至多是n次的多项式pn,使得pn(xi)=yi,i = 0, …, n。
对于这个问题,有一个技巧可以构造插值问题的通用解:

对于这个问题,可以将基函数转化成通用形式:
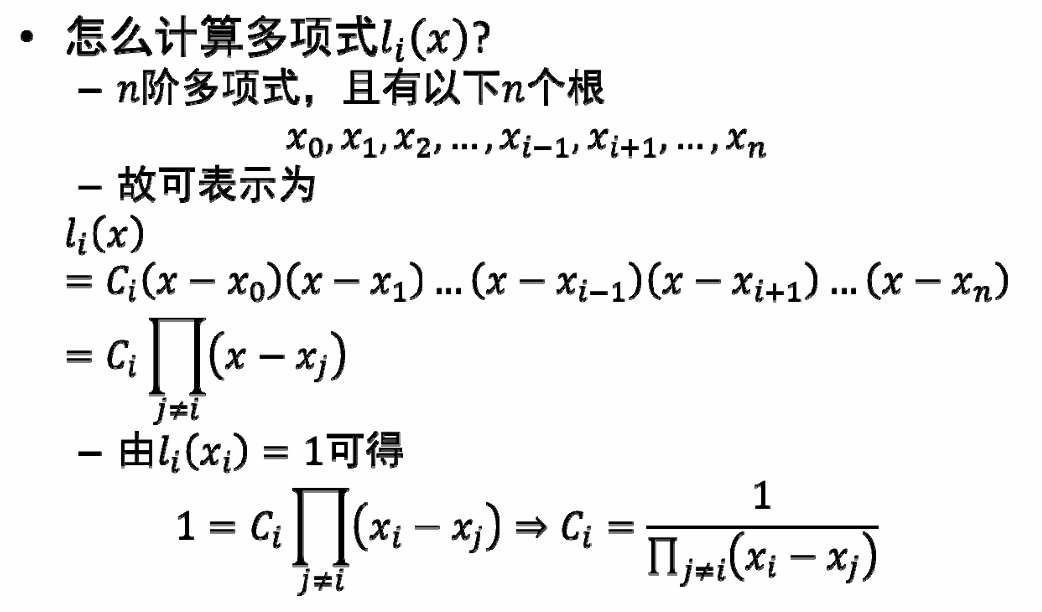
可以得到最终多项式基函数为:

类似的,有另一个技巧是牛顿插值:

多项式插值存在一些问题:
系统矩阵稠密
依赖于基函数选取,矩阵可能病态,导致难于求解(求逆)
病态问题:输入数据的细微变化导致输出(解)的剧烈变化
将线性方程看成超平面,当系统病态时,超平面之间变成近似平行,导致求解(求交)变得困难、不精确
对于矩阵的病态程度,一般用矩阵条件数表示:
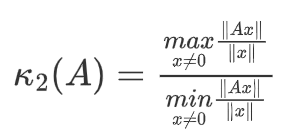
- 矩阵条件数等于最大特征值与最小特征值之间比例
- 条件数大意味着基元之间有太多相关性
多项式插值问题是病态的
对于等距分布的数据点,范德蒙矩阵的条件数随着数据点n呈指数级增长(多项式的最高次数为n-1)
出现这个问题的原因是用幂函数作为基函数,但幂函数之间的差别会随着次数增加而减小
为了解决这个问题,经验是需要系数有正有负,让函数互相抵消
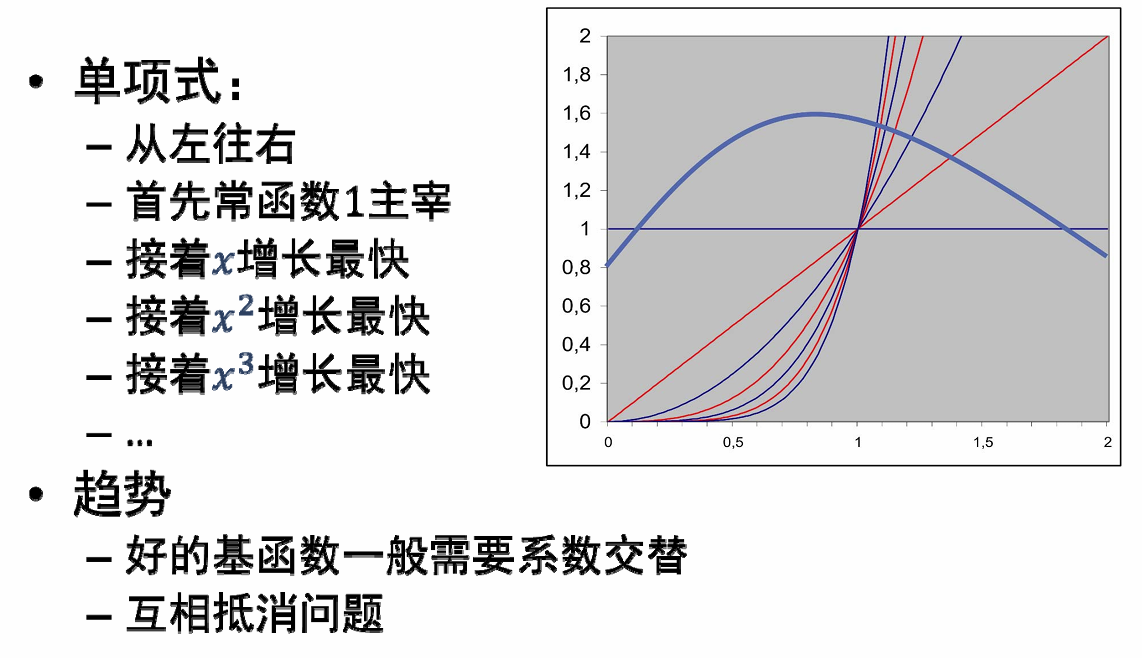
解决方法也就是:
多项式插值结果:
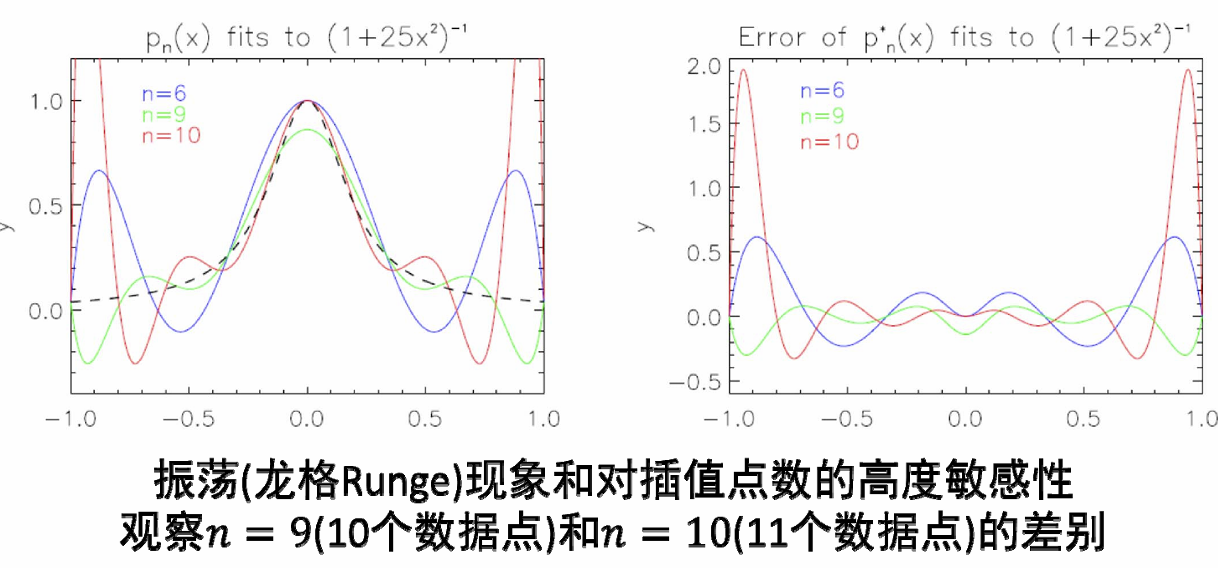
可以得出结论
- 多项式插值不稳定
- 点的微小变化会导致完全不同的结果
- 会出现震荡现象
- 多项式随着插值点数增加而摆动
- 需要用更好的基函数来做插值
- 如Bernstein基函数或分片多项式
- 多项式插值不稳定
多项式逼近
用多项式逼近的原因:
- 数据包含噪声、outlier等
- 可以实现更紧凑的表达
- 计算简单、更稳定
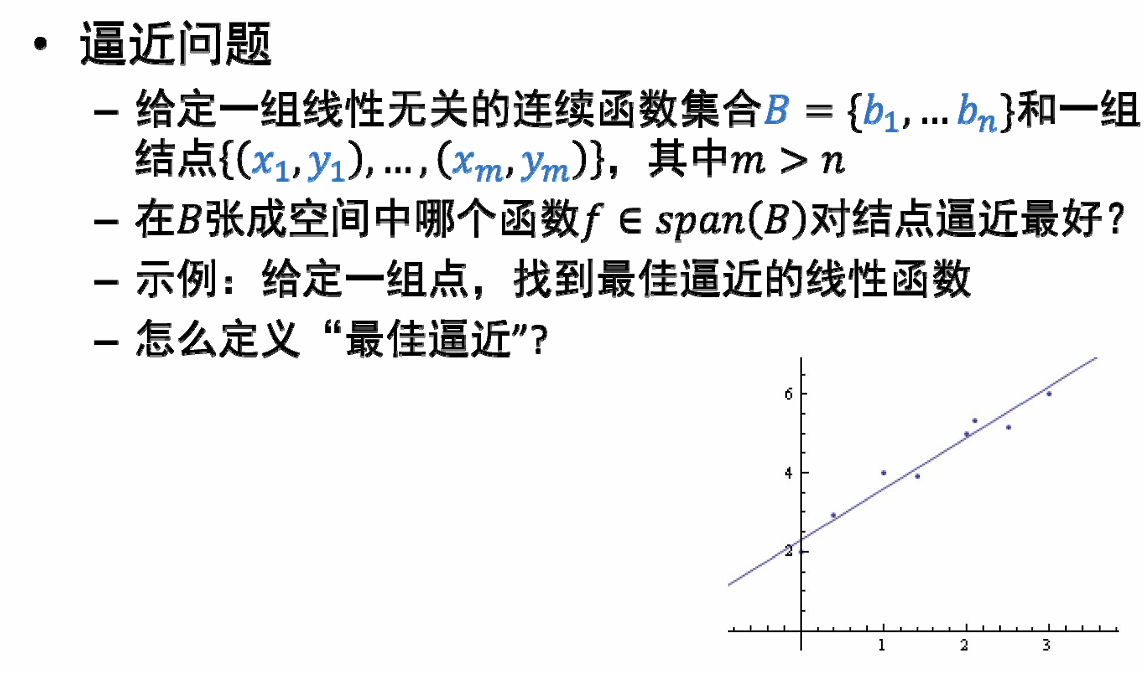
最佳逼近可以定义为:
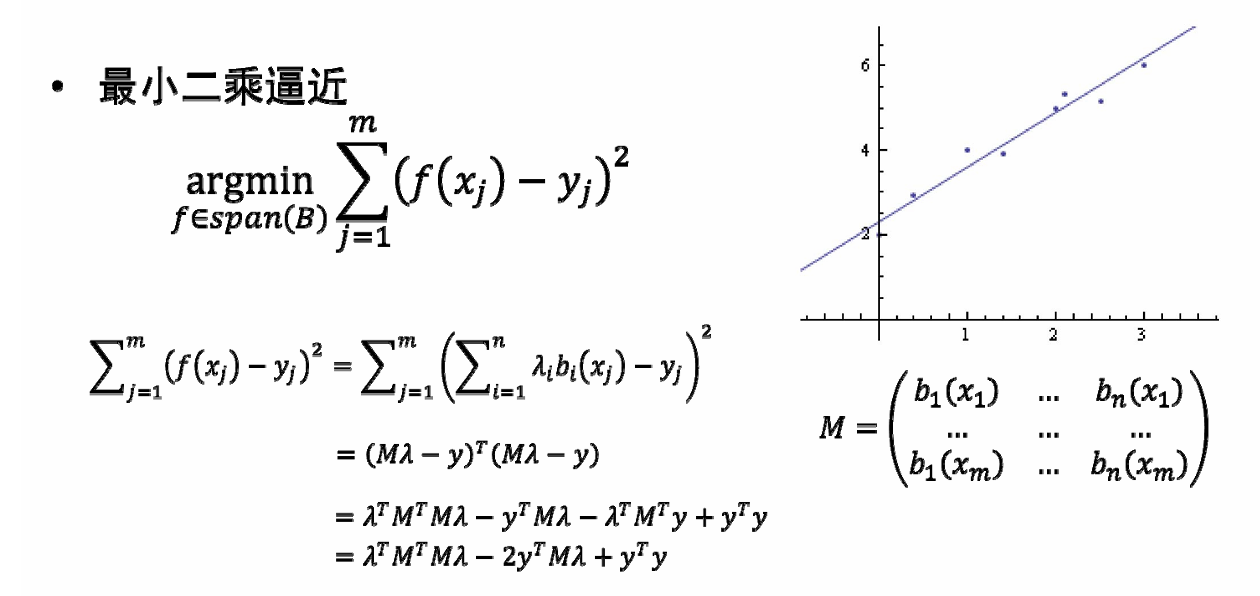
求解过程:

函数空间及基函数
多项式的稠密性与完备性保证了表达能力足够
- 威尔斯特斯拉定理(Weierstrass定理):只证明了存在性,未给出多项式
- 闭区间上的连续函数可用多项式级数一致逼近:对于任意给定的连续函数f(x),以及任意小的正实数ε,存在一个多项式函数P(x),使得在闭区间a,b上,对于任意的x∈[a,b],都有∣f(x)−P(x)∣<ε成立。
- 闭区间上周期为2π的连续函数可用三角函数级数一致逼近:对于以2π为周期的连续函数,存在三角多项式序列一致收敛于该函数。
- 伯恩斯坦(Bernstein)多项式:
- 伯恩斯坦多项式是定义在闭区间[0,
1]上的有界函数f的多项式序列,其表达式为:
- 括号中表示从n(k)个不同元素中取k(n)个元素的组合数
- 恩斯坦证明的关键在于,对于任意连续函数f在区间[0, 1]上,构造出的伯恩斯坦多项式序列Bn(f)会随着n趋向无穷大而一致收敛到f。
- 即对于任意的ε>0,存在一个N,使得对于所有n>N,有∥f−Bn(f)∥<ε
- 伯恩斯坦(Bernstein)基函数的良好性质:非常好的几何意义!
- 正性、权性(和为1) → 凸包性
- 变差缩减性
- 递归线性求解方法
- 细分性
- …
- 伯恩斯坦多项式是定义在闭区间[0,
1]上的有界函数f的多项式序列,其表达式为:
RBF函数插值/逼近
在高维中叫RBF,在一维中叫高斯函数。
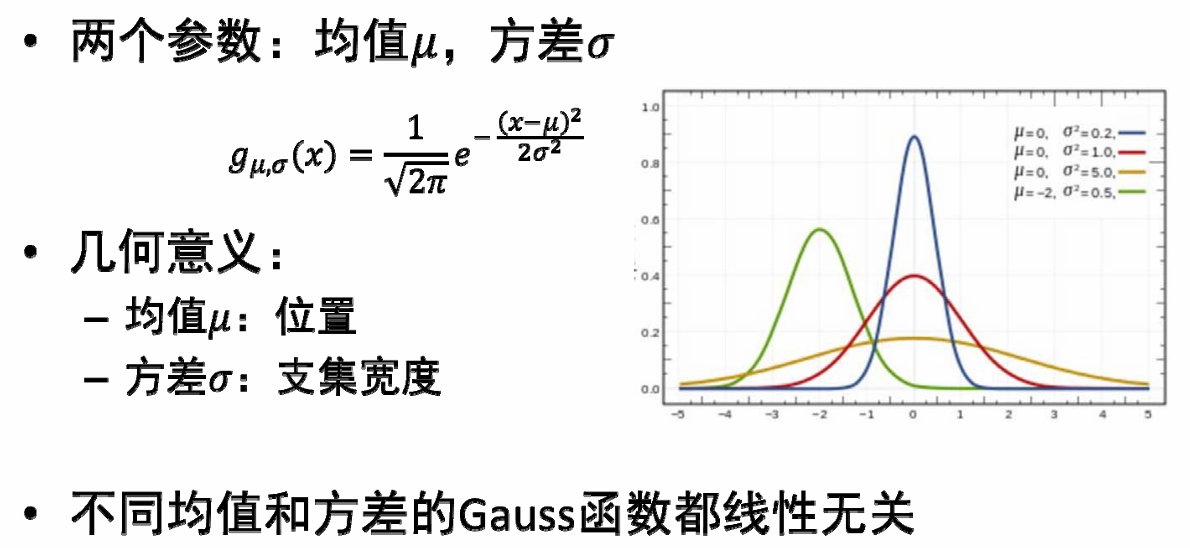
RBF函数:
如果把均值、方差一起优化,就可以更好的拟合函数:
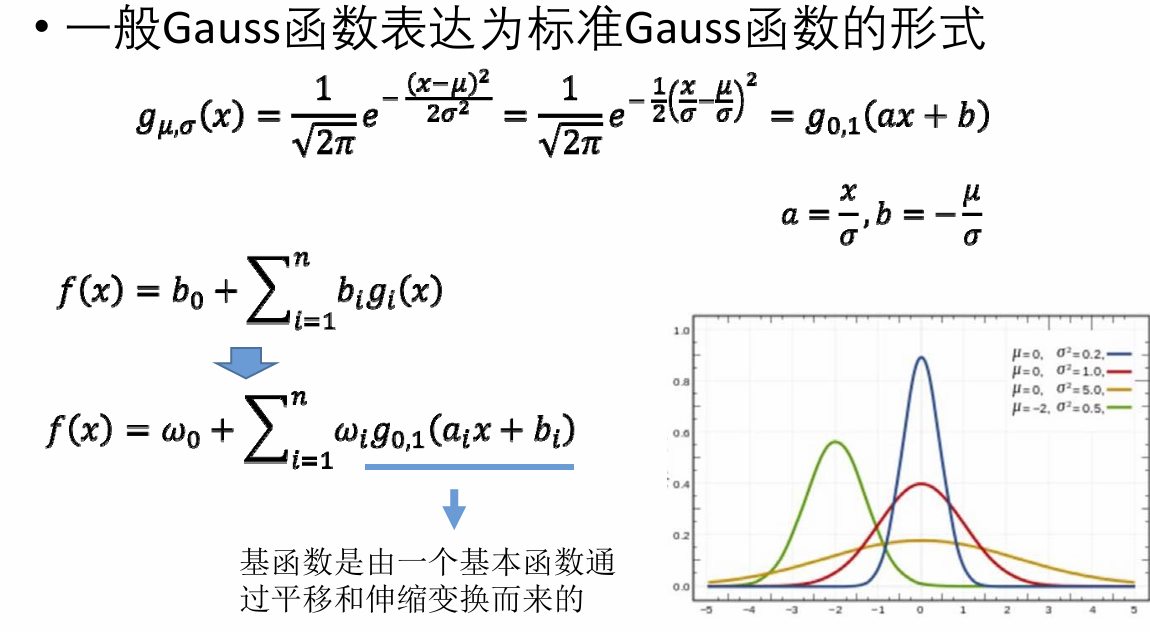
或者,可以把函数看成神经网络参数:
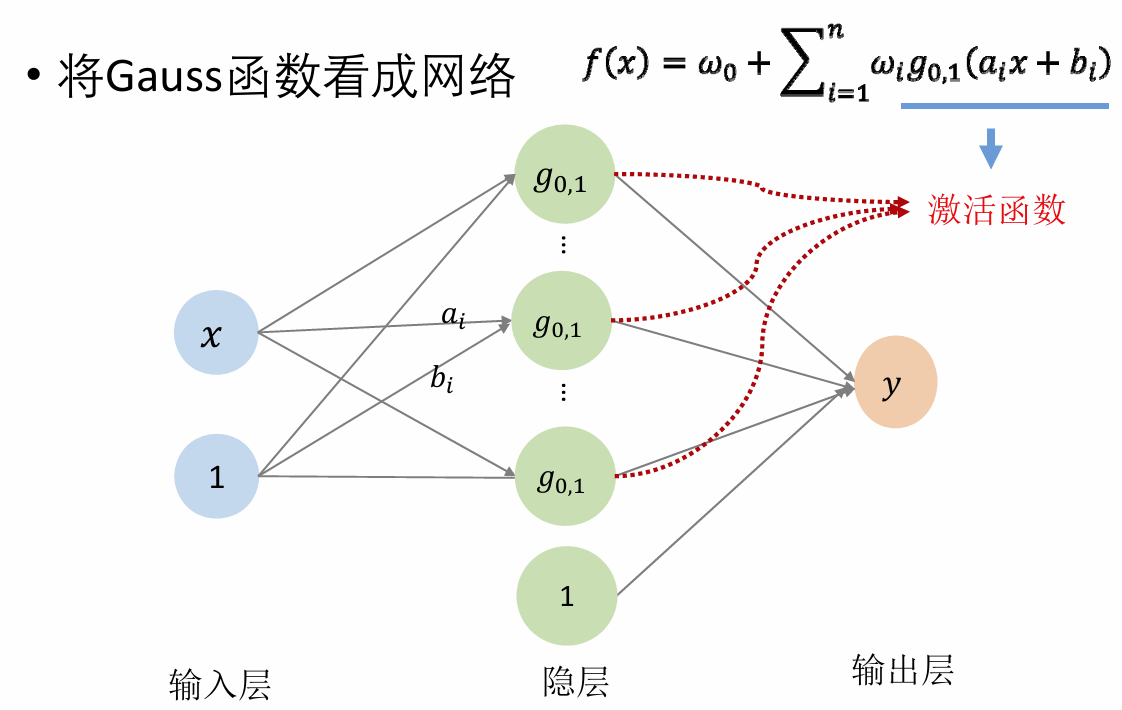
RBF神经网络:
- 输入层:接收输入数据
- 隐含层:由RBF神经元组成,每个神经元对应一个RBF函数,通常采用高斯函数
- 输出层:通常是线性组合的输出,可以是单个神经元或者多个神经元,取决于任务的需求
- RBF神经网络的训练通常分为两个阶段:
- 中心和宽度的选择:可以通过聚类算法(如K-means)来确定中心点 cc,宽度 σσ 可以通过优化算法确定。
- 线性参数的训练:一旦确定了RBF函数的参数,就可以通过线性方法(如最小二乘法)来训练输出层的权重。
一些激活函数的选择:
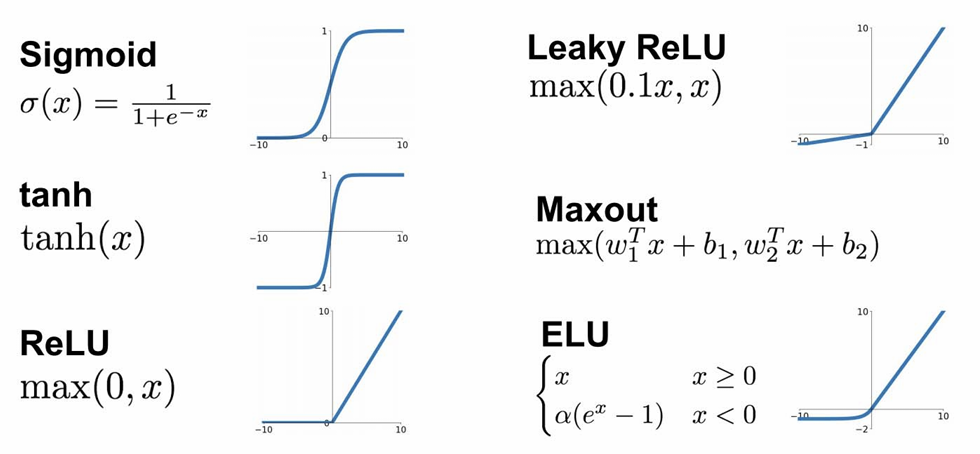
那么,多层神经网络也就是多重复合的函数(包含线性函数和非线性函数)
万能逼近定理:自由度足够多 → 和传统拟合一样存在的问题:函数个数如何选


