GAMES102-01-课程介绍

Lecture 01 Overview

开始学习新的课程，GAMES102内容是几何建模与处理，和GAMES101同步学习。

计算机图形学：表达和表现三维数字对象，构建和创造（虚拟）平行世界。

图像是由像素表达的一些离散的点，图形是由点表达的一些几何元素（图形有时也叫矢量）。

因此矢量图能做到超分辨率

矢量图形的光栅化：扫描转化

渲染成像：光的计算科学

• 解积分方程
• 必须有光源
• 真实感渲染：照片级的渲染

仿真动画：运动的计算科学

• 各种力学方程、流体方程等（偏微分方程）
• 真实感仿真：物理级的运动

图形学面临的问题：数据从哪来？（几何内容的生成）

GAMES102会涉及到的一些数学内容：

• 集合
• 线性空间
  • 每个元素表达为n个实数，即一个向量
• 映射
• 函数
• 赋范空间
  • 内积诱导范数、距离
  • 度量空间：可度量函数之间的距离
  • 空间的完备性：这个函数空间是否可以表示（逼近）任意函数
  • 赋范空间 + 完备性 = 巴拿赫空间
  • 内积空间（无限维）+ 完备性 = 希尔伯特空间

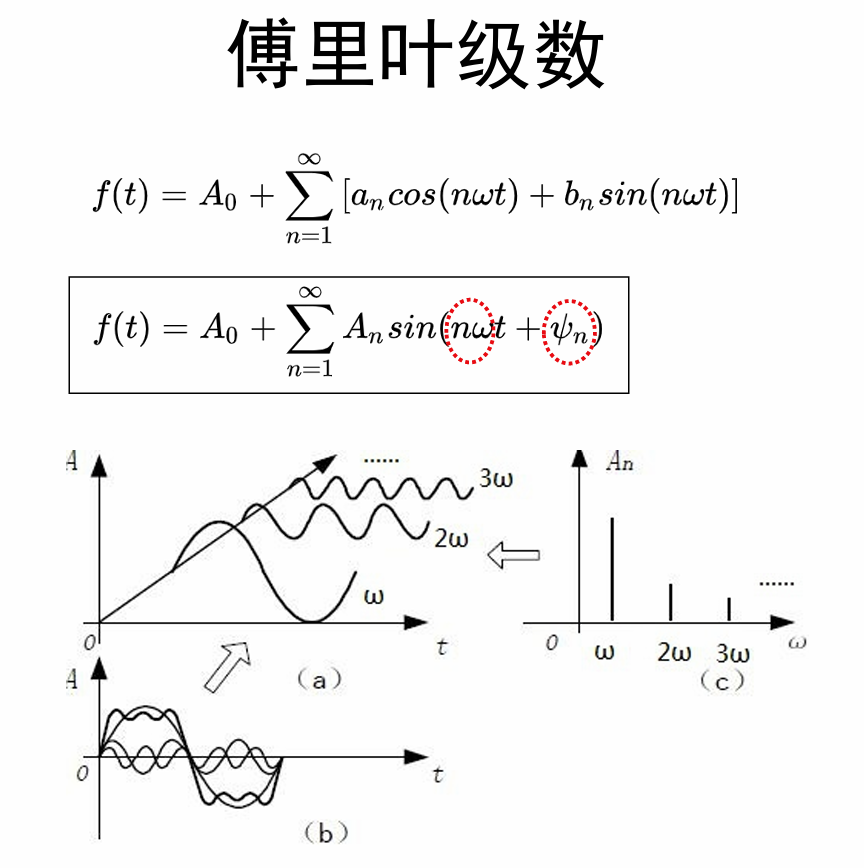
任何一个周期函数都可以写成cos和sin的组合

• 输入不一样、变量不一样、维数不一样
• 如何找函数的三部曲：
  • 到哪找？
    • 确定某个函数集合/空间
  • 找哪个？
    • 度量哪个函数的好的/“最好的”
  • 怎么找？
    • 求解或优化：不同的优化方法与技巧

​ 【注】这里暂定为单变量的函数形式

例子1：逆向工程

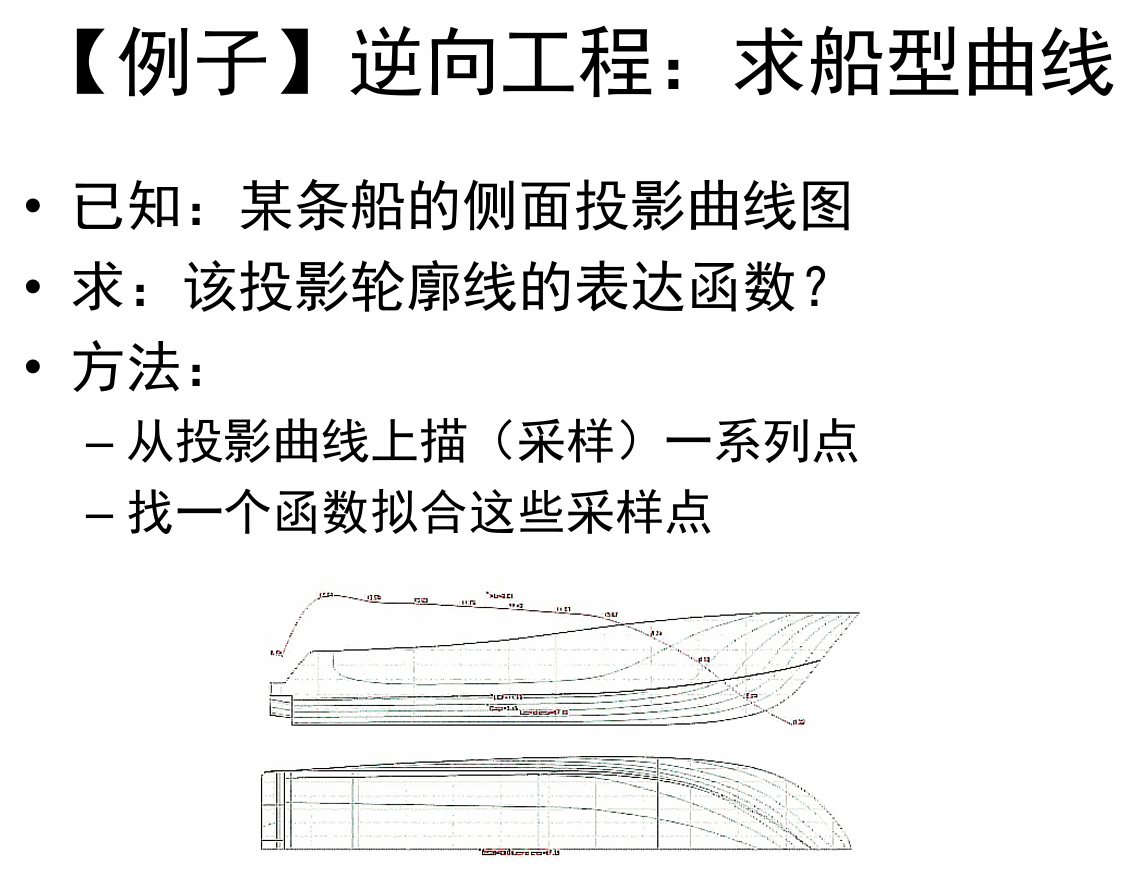
例子2：曲线/曲面拟合问题

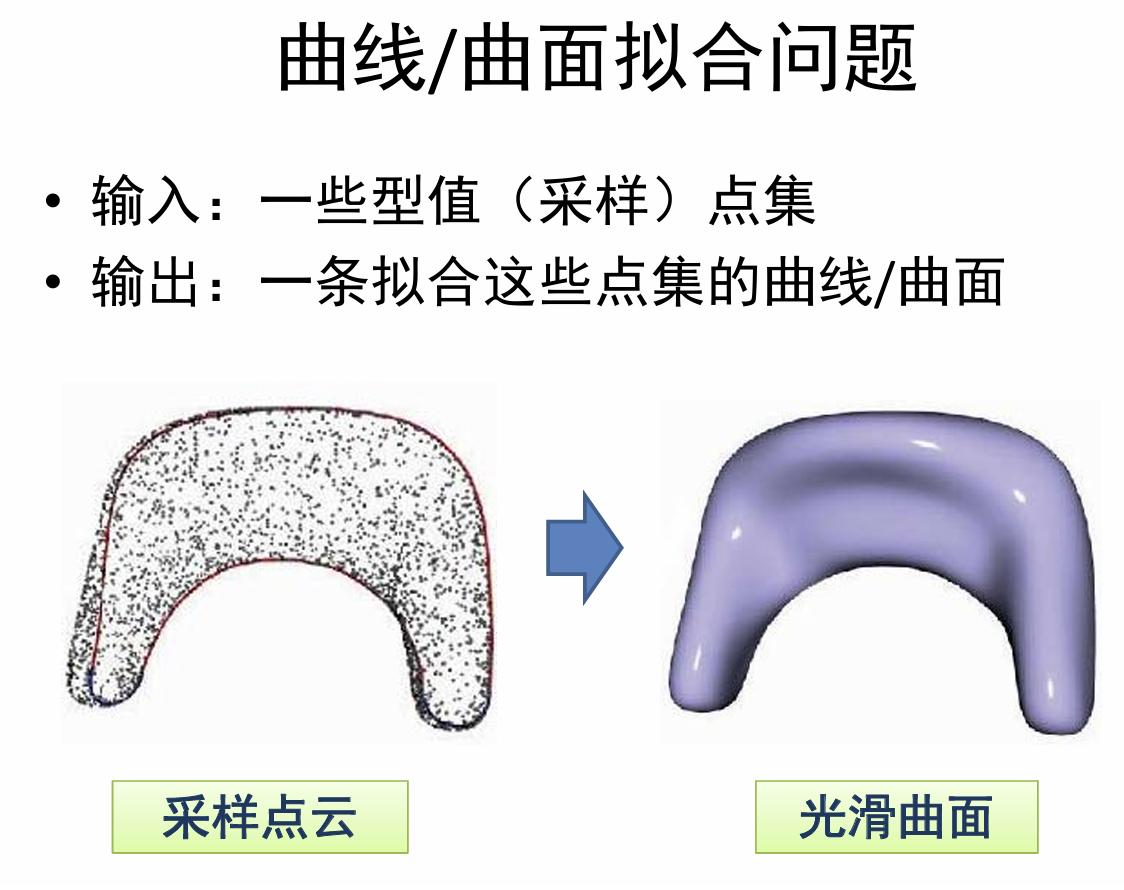
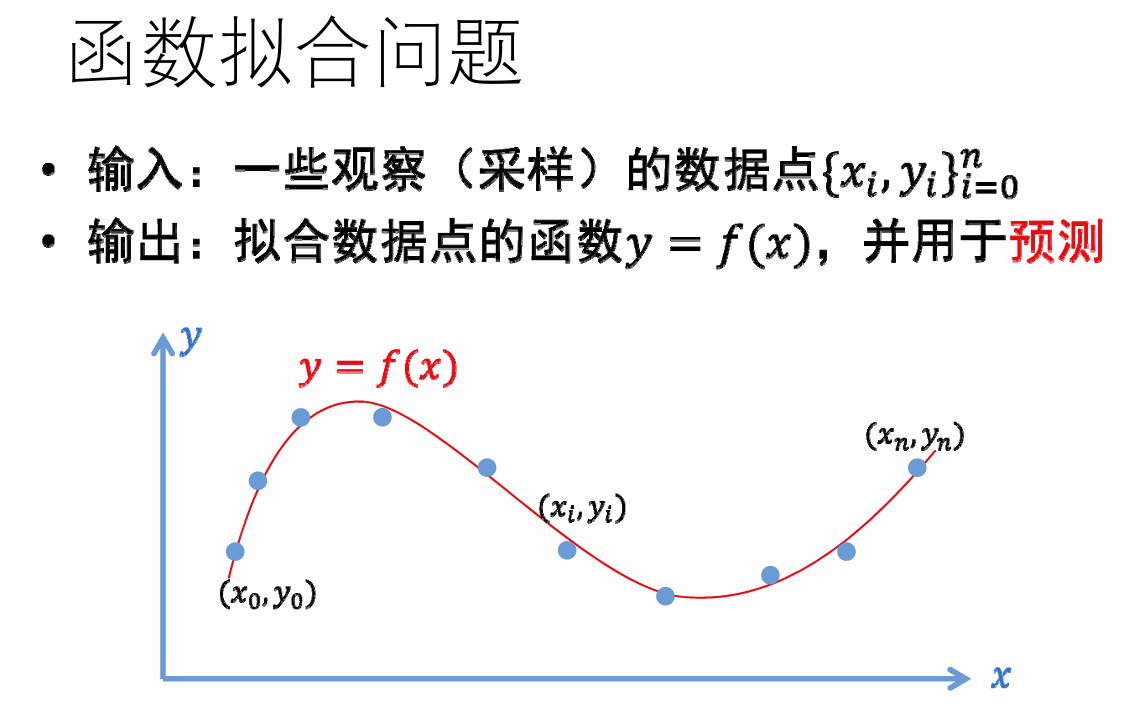
拟合问题：

• 输入：一些观察的数据点
• 输出：反映这些数据规律的函数 y = f(x)

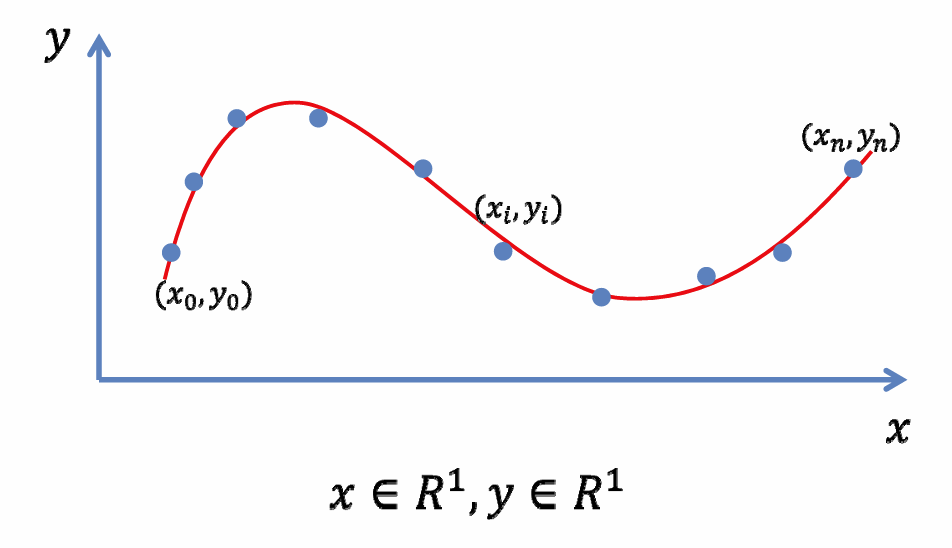
如何找函数的三部曲：

• 到哪找？

  • 选择一个函数空间

• 找哪个？

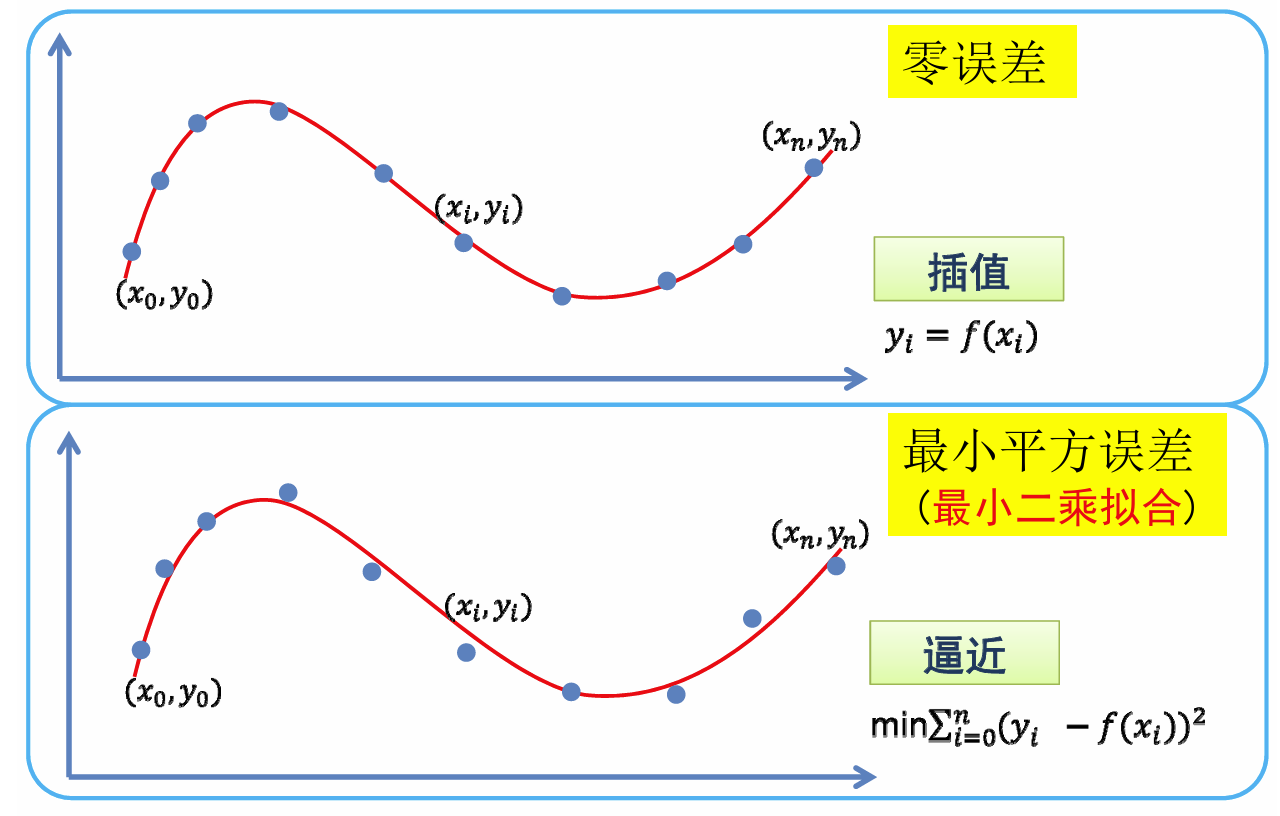
  • 目标1：函数经过每个数据点都插值（零误差）
    • 联立，求解Lagrange插值函数
    • 插值n+1个点、次数不超过1的多项式是存在且唯一的
      • （n+1个变量，n+1个方程）
      • 插值函数的自由度 = 未知量个数 - 已知量个数
  • 目标2：函数尽量靠近数据点（逼近）
    • 设置度量方法，如最小二乘法（适合求导得法方程Ax = b）

  

• 怎么找？

  • 求解或优化：不同的优化方法与技巧
    • 函数尽量靠近数据点（逼近）
    • 最小二乘法

为了减少过拟合和欠拟合，需要根据不同的应用和需求，不断尝试（不断调参）

岭回归：希望稀疏的模小一些，让回归问题更稳定

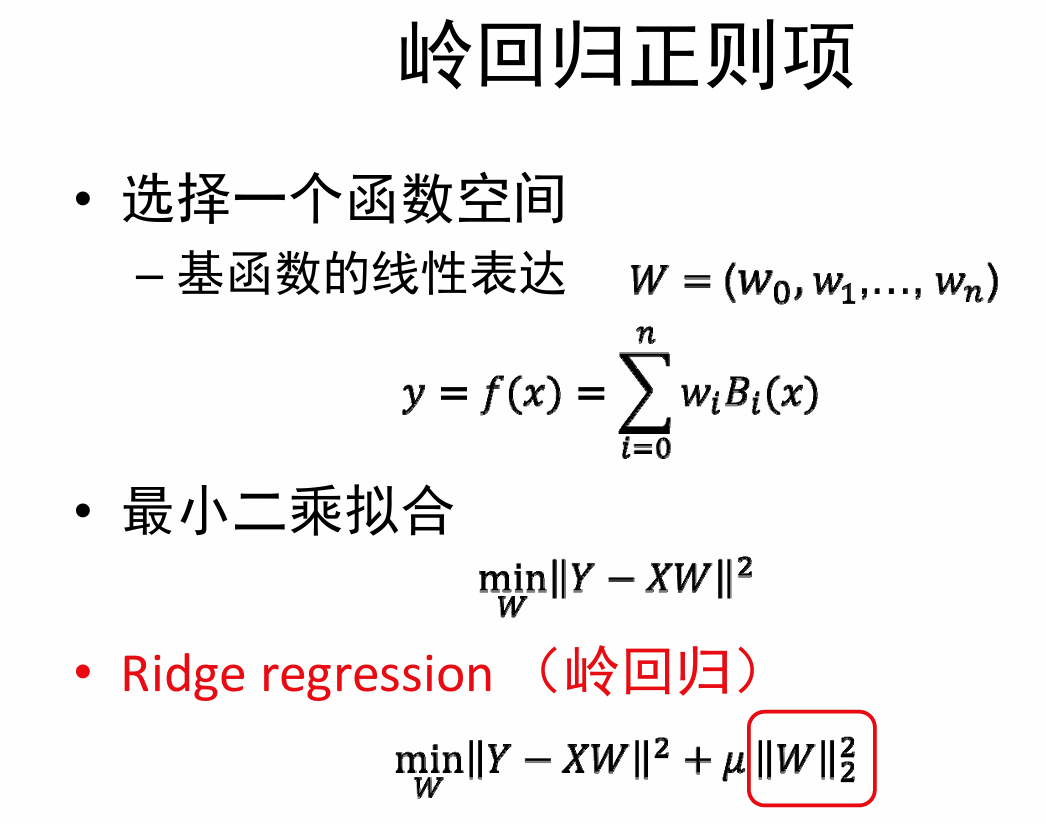
让大多数基函数为零，仅保留少数重要的基函数

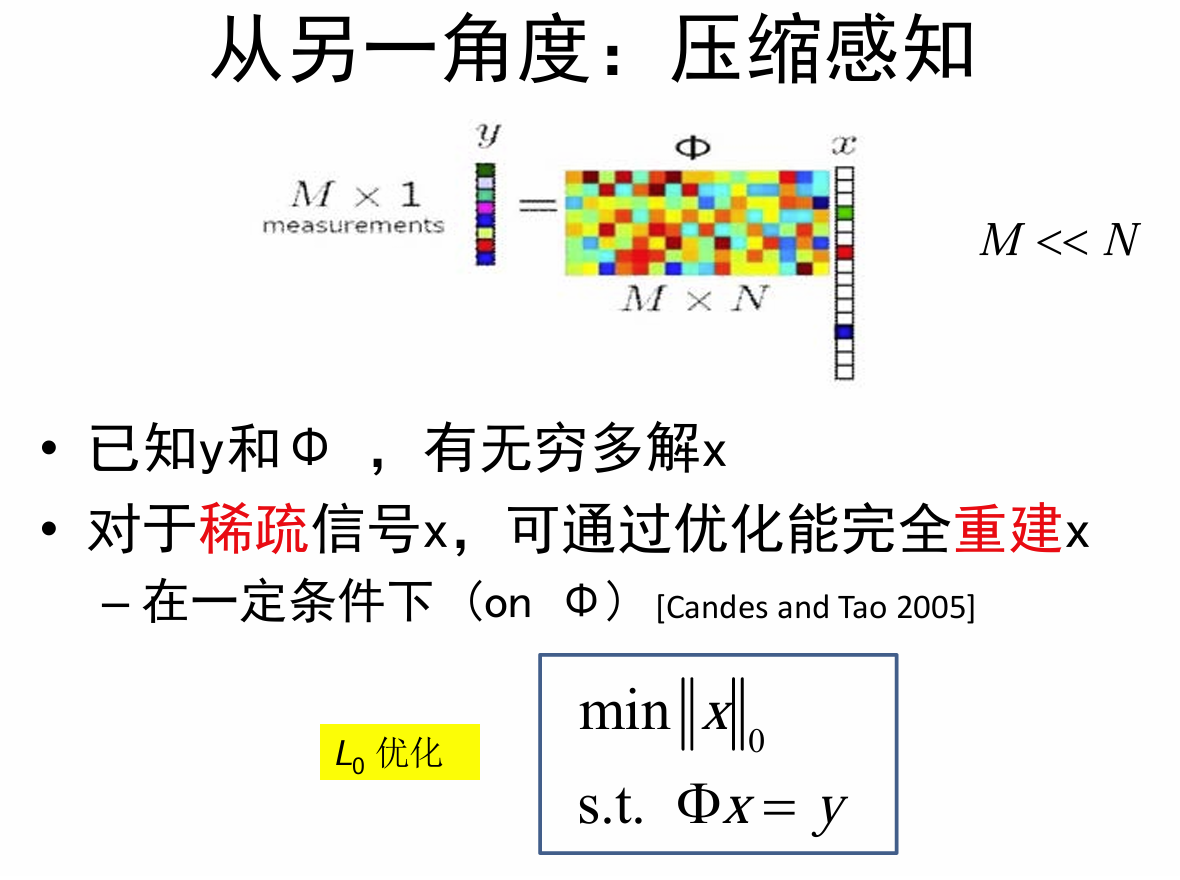
在信号未被完全采样的情况下，通过少量的测量值恢复出原始信号。（证明非常数学）