点云基础及ICP方法介绍

因为实验室组会要求大家介绍一些技术或问题，我想刚好也可以作为第一篇有关研究领域的内容。今天这篇博客会介绍有关点云的一些基本内容。

什么是点云

点云数据是由激光扫描、摄影测量、三维扫描等技术获取的三维空间数据集合，每个点都包含了位置信息以及可能的其他属性，如颜色、法向量等。这些点的密度和分布可以描述一个物体或场景的形状、表面、纹理等信息。点云数据的高精度和丰富的信息使其成为现代科技和工程领域的重要数据来源。

点云的好处

点云数据相比其他数据类型有许多优点和好处，主要体现在以下方面：

1. 三维信息完整：

点云数据以三维坐标的形式表示物体表面上的点，能够完整、准确地记录物体的形状、结构和表面细节，比二维数据更加全面。

2. 高精度和高分辨率：

点云数据通常具有高精度和高分辨率，可以捕捉到微小尺度的细节和变化，适用于需要高精度测量和分析的应用场景。

3. 非接触式测量：

点云数据的采集通常是非接触式的，不需要与物体直接接触，可以避免损伤或改变物体的形状。

4. 快速数据获取：

现代激光扫描仪和相机等设备能够快速获取大量的点云数据，因此可以在较短的时间内完成物体测量，提高工作效率。

​ 5. 多功能性：

点云数据提供了一种数字化的表示方式，可以在计算机中进行存储、处理和分析，可以用于各种后续应用，例如基于点云的三维建模、比较分析等。

点云的常见任务

• 点云的处理： 对采集得到的点云数据进行去噪、滤波、采样等预处理操作，以提高数据质量和后续处理的效果。

• 分割与分类： 将点云数据分割成不同的部分或对象，并对这些部分进行分类，如地面、建筑物、植被等，以便进行场景理解、模型构建等应用。

• 配准与重构： 将多个点云数据进行配准和融合，以获取更完整、更准确的三维信息，并进行曲面重构或体素化，以生成更加真实和可用的三维模型。

点云配准

我分享的主要内容就是点云配准问题。（刚性）点云配准就是通过两个坐标系之间的变化矩阵（包含旋转和平移），将一个数据点云的坐标匹配到另一个数据点云的坐标下，从而达到两片点云坐标的一致性。

点云配准的本质就是：

• 从几何关系来说就是使具有共视关系点云的空间距离足够小，接近于零；

• 从空间分布关系来说，就是最大化共视关系的点重合部分的概率分布。

点云配准的核心其实是向量，因为点的信息只能刻画位置，而向量既包括位置信息又包括姿态信息。而线性代数知识告诉我们：只要找到三维空间的一组基，就可以利用这组基表示三维空间下的任意向量。点云配准是计算两个具有共视关系点云的变换关系，点云中的每个点都可以理解成与某一个点的连接而成向量，因此我们所要求的变换关系也就是坐标系的变换关系。

ICP方法

ICP（Iterative Closest Point，迭代最近点）是最为经典的配准方法之一。

经典ICP方法包含对应点搜索和变换估计两个阶段：

• 对应点搜索是指在两帧点云中找到每个点的匹配点；

• 变换估计就是利用对应关系来估计变换矩阵。

这两个阶段将不断进行迭代，使得对应关系越来越准确，从而找到最佳的变换矩阵。

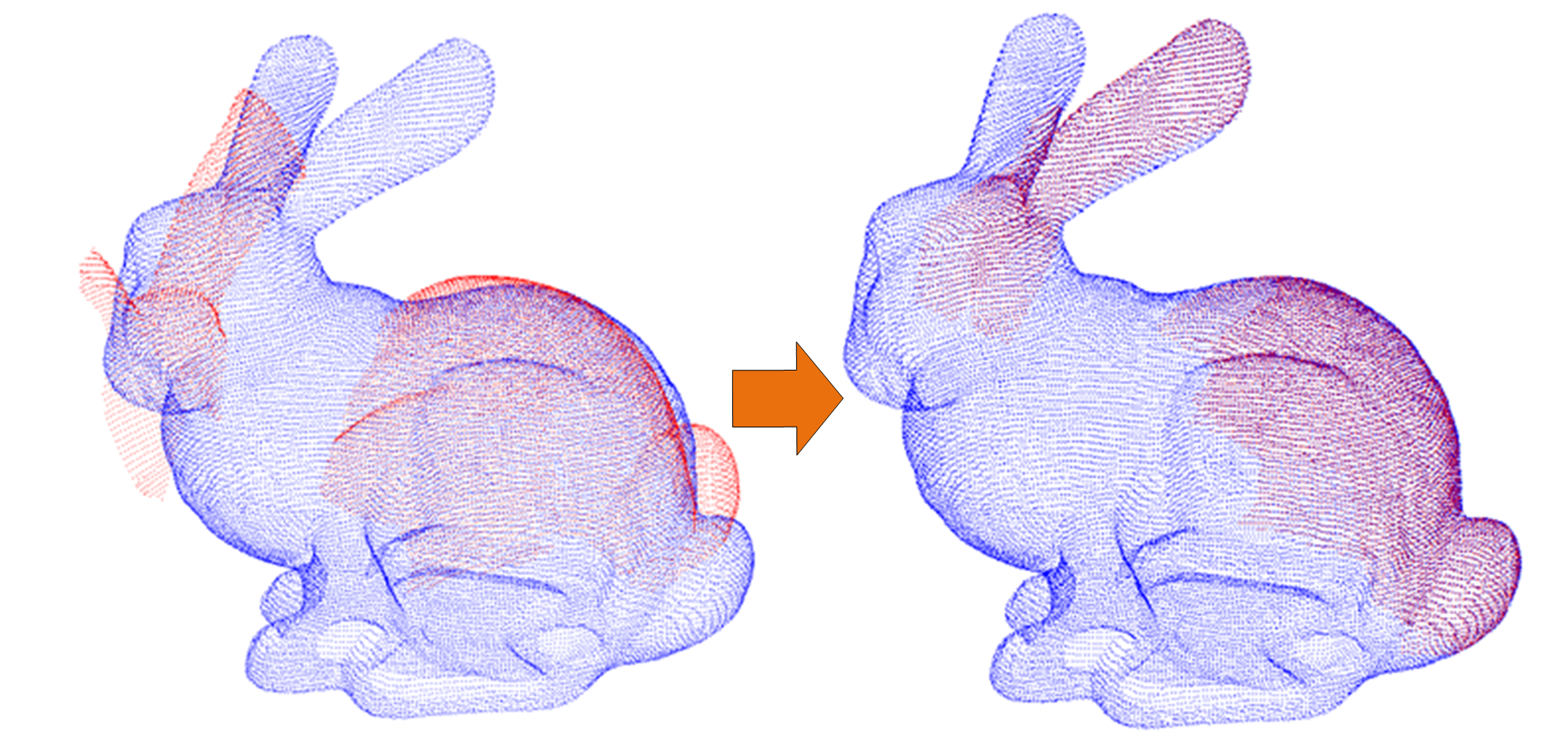
ICP算法核心是最小化一个目标函数，实际上就是所有对应点之间的欧式距离的平方和。

在粗配准（也就是得到一个初始的旋转平移矩阵）后，用初始的旋转平移矩阵对原始进行变换得到的一个变换后的点云，然后将这个变换后的点云与目标点云进行比较，只要两个点云中存在距离小于一定阈值（最邻近点），就认为这两个点就是对应点。

有了对应点之后，用对应点对旋转R与平移T进行估计，优化得到了一个新的R和T。新的R和T会导致一些点转换后的位置发生变化，一些最邻近点对也相应的发生了变化。然后又回到寻找最邻近点的步骤不停迭代进行，直到满足一些迭代终止条件，如R、T的变化量小于一定值，或者目标函数的变化小于一定值，或邻近点对不再变化等。

这里的优化过程其实是一个贪心策略。首先固定R跟T利用最邻近算法找到最优的点对，然后固定最优的点对来优化R和T，依次反复迭代进行。这两个步骤都会使得目标函数值下降，所以ICP算法总是收敛的。

在ICP算法中参数主要有两个，一个是ICP的邻近距离，另外一个是迭代的终止条件。参数的选择，与实际的工程应用相关。比如说你的仪器精度是5mm，那么小于5mm是可以认为是对应点，而最终的迭代终止条件也就是匹配点之间平均距离小于5mm。

ICP方法简单直观，不需要训练数据，可以较好地推广到未知场景。但ICP算法存在一些问题：

• ICP方法在搜索对应点的过程中遍历了所有点云，在点云数量较大时计算量将爆炸增长。
• 对配准点云的初始位置有一定要求，不合理的初始位置会导致算法陷入局部最优。
• ICP算法在寻找对应点时，模型会将任何两个点云之间的欧氏距离最近的点作为对应点，这种假设会产生一定数量的错误对应点。

为了解决ICP方法中的这些问题，出现了一些ICP的改进算法，但它们也只是解决了一部分问题。包括降低计算量但仍会陷入局部最优的的特征点ICP方法、避免局部最优但计算速度较慢的点到面ICP，面到面ICP方法等。

这篇文章的内容大致就是这些。对于点云配准问题，除了ICP这类基于优化的方法外，还有一些其它的方法，如基于特征的方法，基于学习的方法等，在后续都会有涉及。不出意外的话，下一篇有关点云的博客会是我在组会介绍的另一篇基于学习的点云配准论文。